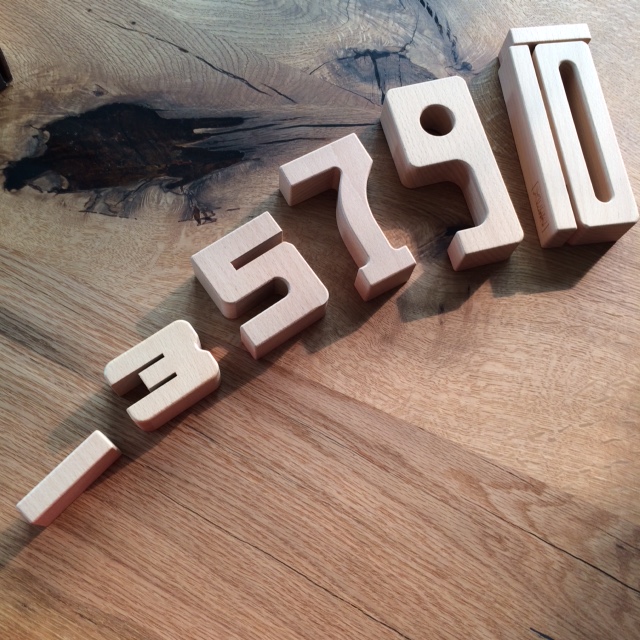Zahlenbausteine sind nach wie vor ein ziemlich geniales Material zum Eintauchen in die Welt der Mathematik. Mittlerweile gibt es da auch mehrere Anbieter mit den unterschiedlichsten Designs dieser Bausteine. Im heutigen Blogbeitrag werde ich 5 verschiedene Produkte der Zahlenbausteine beispielhaft für euch testen und vergleichen. Bestimmt findet ihr noch mehr solcher Anbieter und dann könnt ihr meine Vergleichs-Kategorien ja einfach darauf übertragen und euch so immer wieder selbst ein Gesamturteil bilden. Ach ja und auch dieser Hinweis muss wieder sein: Es handelt sich hierbei um Produktwerbung.
Also los gehts! Folgende 5 Anbieter gehen ins Rennen:
Zahlenbausteine von ASTRUP hier z.B. bei Hase Weiss entdeckt

Zahlenbausteine von Calculix

Rechenbausteine von Eichhorn (auf Amazon gefunden)

Zahlenbausteine von SumBlox

Stapelzahlen von Wissner

Wenn wir uns die Zahlenbausteine – wie auf dem unteren Foto – genauer anschauen, dann fallen sofort Unterschiede auf: z.B. die Ziffernformen, die Größen oder auch die Farbgestaltung. Also ist es sinnvoll die Zahlenbausteine auf bestimmte Kategorien hin zu betrachten. Ich habe mir folgende überlegt: die Zahlenform, die Farbe & Optik, die Haptik, die Stapelbarkeit, den Umfang & die Ausstattung eines Standard-Sets, das didaktische Potenzial, das Preis-Leistungs-Verhältnis (Kosten je Baustein) sowie eventuelle Besonderheiten des Produktes.

Fangen wir mit der Zahlenform an, welche meines Erachtens eine enorme Bedeutung hat:
| ASTRUP Wodden Numbers | Die kleinen Zahlen wirken vergleichsweise sehr realistisch. Die großen Zahlen sind jedoch sehr stark gestreckt. Sie wirken daher unförmig und unrealistisch. |
| Calculix Zahlenbausteine | Hier haben wir sehr realistische und ästhetisch wirkende Zahlenformen mit einem gutem Verhältnis zwischen Streckung und Zerrung. |
| Eichhorn Rechenbausteine | Die Zahlenformen sind sehr schwer erkennbar. Die Zahl an sich wird oft erst durch die Lackierung deutlich. |
| SumBlox Matheblöcke | Einige Zahlen sind gut gelungen. Andere Zahlen sind jedoch sehr abstrakt. Zu geringe Radien und die zu dicke Linienstärke führen dazu, dass manche Bausteine nicht so realistisch wirken. |
| Wissner Stapelzahlen | Die Zahlenform an sich ist sehr gut erkennbar. Die Bausteine haben oben und unten Stapel-Balken, wodurch die Bausteine insgesamt keine Zahlenform aufweisen, was sie natürlich auch nicht müssen. |
Mein Zwischenfazit an dieser Stelle: Die Zahlenform bei Calculix und bei Wissner entsprechen am besten den im Alltag verwendeten sowie im vorschulischen Kontext und im Mathematikunterricht der Grundschule genutzten Ziffernformen.
Schauen wir uns die Farbe & Optik an:
| ASTRUP Wodden Numbers | Ansprechende und neutrale Holzoptik, sehr gleichmäßig und glatt lackiert. |
| Calculix Zahlenbausteine | Durch die Ölung kommen Holzfarbe und Struktur wunderbar zum Vorschein. |
| Eichhorn Rechenbausteine | Die Bausteine sind aus meiner Sicht zu bunt lackiert. |
| SumBlox Matheblöcke | Ansprechende und neutrale Holzoptik, sehr gleichmäßig und glatt lackiert. |
| Wissner Stapelzahlen | Es gibt sie in den Montessori-Farben (vgl. Foto) und in Naturfarbe. Beide Versionen wirken durch das RE-Wood-Naturmaterial sehr harmonisch. |
Mein Zwischenfazit: Bei Farbe und Optik fallen die Rechenbausteine von Eichhorn leider durch.
Weiter geht es mit der Haptik:
| ASTRUP Wodden Numbers | Man spürt, dass es Holz ist. Die Zahlen sind jedoch stark lackiert, was das Holzgefühl schmälert. Die Zahlen sind recht dünn, können aber gut ertastet werden. |
| Calculix Zahlenbausteine | Tolle Haptik, da das Holz nur geölt ist. Dadurch bleibt die Holzstruktur fühlbar. Die massiven Zahlen lassen sich sehr gut ertasten. |
| Eichhorn Rechenbausteine | Man spürt am Gewicht und an der „Wärme“, dass es Holz ist. Die Zahlen sind sehr stark lackiert. Die Zahlenformen können kaum ertastet werden. |
| SumBlox Matheblöcke | Man spürt, dass es Holz ist. Die Zahlen sind lackiert, was das Holzgefühl jedoch nicht schmälert. Die Zahlen sind massiv und lassen sich mit den abgerundeten Kanten sehr gut ertasten. |
| Wissner Stapelzahlen | Trotz Re-Wood-Material (zerkleinerte Holzreste) ist es eher ein Kunststoff-Feeling, aber ein schönes Gewicht. Durch die Balken sind die Zahlen zwar nicht so gut ertastbar aber man kann die einzelnen Formen gut mit Fingern auf den Rillen nachfahren. |
Mein Zwischenfazit hier lautet: Ich persönlich liebe Holz und mir ist eine gute Haptik sehr wichtig, die von Calculix und SumBlox voll erfüllt wird. Aber auch die Stapelzahlen von Wissner haben etwas besonderes durch die Balken und die „Rillen“.
Die nächste Kategorie ist die Stapelbarkeit.
| ASTRUP Wodden Numbers | Die Zahlen sind zu dünn, zu schmal und zu lang, so dass sie sich nur sehr schwierig und wackelig stapeln lassen. |
| Calculix Zahlenbausteine | Die Zahlen sind trotz größerer Radien gut stapelbar. Die geölte Holzstruktur verbessert die Stapelbarkeit zusätzlich, da sie weniger rutschen. |
| Eichhorn Rechenbausteine | Die Zahlen sind gut stapelbar aber durch die Lackierung etwas rutschig. |
| SumBlox Matheblöcke | Die Zahlen sind gut stapelbar. |
| Wissner Stapelzahlen | Die Zahlen lassen sich durch die Balken sehr gut stapeln. |
Im Zwischenfazit zur Stapelbarkeit fallen die Zahlenbausteine von ASTRUP hier leider durch.
Kommen wir zu einer weiteren sehr wichtigen Kategorie, nämlich zum Umfang und zur Ausstattung eines Standard-Sets.
| ASTRUP Wodden Numbers | 15 Zahlenbausteine: je 2 x 1 bis 5, je 1 x 6 bis 10 |
| Calculix Zahlenbausteine | 61 Zahlenbausteine: 20 x 1, 10 x 2, 7 x 3, 5 x 4, 4 x 5, 4 x 6, 3 x 7, 3 x 8, 3 x 9, 2 x 10 |
| Eichhorn Rechenbausteine | 9 Zahlenbausteine (jede Zahl von 1 bis 9 einmal), die Zahl 10 fehlt. |
| SumBlox Matheblöcke | 47 Zahlenbausteine: 14 x 1, je 4 x 2, 3, 4, 5, 6, 7, 8, 9 und 1 x 10 |
| Wissner Stapelzahlen | 34 Zahlenbausteine: 12 x 1, 7 x 2, 4 x 3, 4 x 4, 2 x 5, 1 x 6, 1 x 7, 1 x 8, 1 x 9, 1 x 10 |
Mein Zwischenfazit hier lautet: Das Basis-Set von Calculix ist mit 61 gut zusammengestellten Bausteinanzahlen (20 Einer und 10 Zweier sind der Wahnsinn!!!) unschlagbar!!!
Weiter geht’s mit dem didaktischen Potenzial, welches mir als Mathematikdidaktikerin besonders am Herzen liegt. Zwei Prinzipien haben alle Produkte gemeinsam: 1. „GLEICHE HÖHE = GLEICHER WERT“ und 2. die sich daraus ergebene Möglichkeit der Eigenverantwortung und Selbstkontrolle beim Spielen und Lernen nach Montessori „Hilf mir es selbst zu tun.“ Was gibt es noch zu den didaktischen Möglichkeiten der Zahlenbausteine der einzelnen Anbieter zu sagen?
| ASTRUP Wodden Numbers | Die ungünstige Form und Stapelbarkeit der Zahlen, die geringe Anzahl der einzelnen Zahlen (insbesondere der Einer) sowie fehlende Begleitmaterialien reduzieren das didaktische Potenzial und den Einsatz im (vor-)schulischen Kontext. |
| Calculix Zahlenbausteine | Die Möglichkeit zur Umsetzung vom Kardinalitätsprinzip durch die 20 Einerbausteine ist einfach genial. Man kann jede Zahl als Menge von Einerbausteinen darstellen. Hinzu kommen die realistischen Zahlenformen und die sehr gute Stapelbarkeit, kombiniert mit einem Anleitungsheft, welches didaktische Tipps zu Spielen und möglichen Rechenarten bereit hält. Und hier noch ein Geheim-Tipp: Bald wird es ein lehrplankonformes Handbuch mit vielen didaktischen Hinweisen und Kopiervorlagen zum Addieren und Subtrahieren geben. |
| Eichhorn Rechenbausteine | Die unrealistischen Zahlenformen, die grellen Farben, die geringe Anzahl der Steine, die fehlende Zahl 10 und fehlende Begleitmaterialien machen dieses Produkt aus mathematik-didaktischer Sicht für mich wertlos. |
| SumBlox Matheblöcke | Die Möglichkeit zur Umsetzung vom Kardinalitätsprinzip durch die 14 Einerbausteine ist auch hier toll. Man kann jede Zahl als Menge von Einerbausteinen darstellen. Hinzu kommt die sehr gute Stapelbarkeit. Ein kleines Manko sind die teilweise etwas abstrakten Zahlenformen, die für einige Kinder problematisch sein können. Einige didaktischen Tipps gibt es auf Spielkarten, die käuflich dazu erworben werden können. |
| Wissner Stapelzahlen | Die Möglichkeit zur Umsetzung vom Kardinalitätsprinzip durch die 12 Einerbausteine ist auch hier toll. Man kann jede Zahl als Menge von Einerbausteinen darstellen. Weitere didaktische Pluspunkte sind: die sehr realistischen Zahlenformen, die Zentimeter-Relation (die 5 ist auch 5 cm groß), die passenden Montessori-Farben, die „Rillen“ zum Nachfahren mit dem Finger und die zusätzlichen 42 Aufgabenkarten mit Lösungen zum Spielen und Lernen, die käuflich dazu erworben werden können. |
Mein Zwischenfazit lautet: Aus didaktischer Sicht können die Zahlenbausteine von Calculix und SumBlox sowie die Stapelzahlen von Wissner sehr gut zum Erlernen des Zahlbegriffs und zum Darstellen von Rechenoperationen genutzt werden.
Als nächstes möchte ich noch einen Blick auf das Preis-Leistungs-Verhältnis (Kosten je Baustein) werfen, welches aber natürlich aufgrund von Preisveränderungen und Aktionen Schwankungen unterliegt.
| ASTRUP Wodden Numbers | Preis: 42,90€ Preis je Baustein: 2,86€ |
| Calculix Zahlenbausteine | Preis: 79,00€ Preis je Baustein: 1,31€ ACHTUNG: Es gibt einen Rabatt-Code am Ende des Beitrages!!! So wird es noch günstiger. |
| Eichhorn Rechenbausteine | Preis: 12,85-17,12€ Preis je Baustein: 1,43-1,90€ |
| SumBlox Matheblöcke | Preis: 79,95€ Preis je Baustein: 1,70€ |
| Wissner Stapelzahlen | Preis: 34,95€ (einfarbig) 49,90€ (farbig) Preis je Baustein: 1,03€ / 1,47€ |
Zum Ende möchte ich gern noch auf einige Produktbesonderheiten eingehen, die bei eurer Kaufentscheidung wichtig sein könnten.
| ASTRUP Wodden Numbers | Es gibt einen Stoffbeutel mit in der Schachtel, der sehr gut für das Erfühlen der Zahlen geeignet ist. |
| Calculix Zahlenbausteine | Das Basis-Set aus FSC Massivholz sowie die Massiv Zahlenreihe werden in der EU produziert. Es gibt auch ein Kompakt-Basis-Set aus Flüssigholz (Arboform). Dieses Set wird in Deutschland in Werkstätten für Menschen mit Einschränkungen produziert und besteht zu 100% aus natürlichem Recycling-Material. Zudem sind die Zahlen dieses Sets in Zentimeter-Relation (d.h. die Zahl 5 ist auch 5cm groß) und sehr leicht, also gut zum Transportieren geeignet. Viele weitere Zusatzmaterialien sind in Vorbereitung. |
| Eichhorn Rechenbausteine | Hier kann ich leider nichts berichten. |
| SumBlox Matheblöcke | Es gibt folgende Zusatzprodukte: Frühkindliche Aktivitätskarten, ein Starter-Set, ein Bildungs-Set und jede Holzzahl (bis 9) kann in beliebiger Anzahl gekauft werden. SumBlox verspricht für jedes verkaufte Set einen Baum zu pflanzen. |
| Wissner Stapelzahlen | Das ökologisch nachhaltige RE-Wood®-Material wird aus zerkleinerten Holzresten deutscher Produktion und einem Bindemittel im Verhältnis 80 zu 20 ressourcenschonend hergestellt. RE-Wood® ist zu 100%-recyclebar, mit dem PEFC-Siegel zertifiziert und frei von Schadstoffen. Die Stapelzahlen entstehen in Kooperation mit regionalen Behindertenwerkstätten. Es gibt Aufgabenkärtchen sowie Sets für den 200er und für den 500er Zahlenraum. |
Ja das hört sich doch alles wirklich interessant und spannend an, oder? Hättet ihr das gedacht? Es lohnt sich also auf jeden Fall immer wieder Produkte vor dem Kauf genauer unter die Lupe zu nehmen.

Bis zum nächsten Beitrag wünsche ich euch alles Gute!
Eure Mandy Fuchs


































































































































































































































 Zahlen ordnen
Zahlen ordnen