Schlagwort-Archive: Matheforscher

Mit Magnetspielzeug Mathe lernen?

2019-11-26 mandyfuchs

Magnetbausteine oder allgemein magnetische Spiel- und Baumaterialien können Kinder wirklich echt faszinieren. Das erlebe ich selbst immer wieder, wenn ich solche Sachen mit in meine Förderprojekte für meine kleinen Matheassen in Kitas und Grundschulen nehme. Damit wird ausdauernd und konzentriert gespielt, experimentiert, geknobelt und jede Menge Mathematik dabei gelernt. Ja ihr habt richtig gelesen! Mit Magnetspielzeug kann man Mathematik lernen und das möchte ich euch im neuen Blogbeitrag vorstellen.

Ja und falls jemand nicht so auf Magnete steht, der schaut einfach bei meinen Vorschlägen für mathematische Spiele und Spielmaterialien oder auch bei meiner Sammlung zu den mathematischen Kinderbüchern vorbei. Hab ich euch gleich nochmal verlinkt. Hier sind mittlerweile schon tolle Sachen zusammen gekommen.

Und auch diesmal muss dieser Hinweis sein: Da ich eine konkrete Marke, nämlich die Magnetteile von GeoSmart ausprobieren durfte, handelt es sich um Werbung. Ihr wisst ja vielleicht, dass ich schon lange mit solchen magnetischen Teilen forschen wollte. Und ich war gespannt, wie viel Mathematik da wirklich drin steckt. Ich bin ja schon Fan von diesem tollen Magnetwürfel hier:

Und auch die Bausätze mit Magnetstäbchen und Magnetkugeln, wie zum Beispiel die hier, haben es mir total angetan:

Mit beiden Materialien (die ich übrigens selbst gekauft habe) habe ich schon so manche tolle Matheasse-Förderstunde durchgeführt.

Heute geht es aber um die Magnetteile von GeoSmart.

Ich hatte den Space Ball mit seinen insgesamt 36 Teile: 18 Quadrate, 4 Trapeze, 12 Dreiecke, ein Led-Modul und ein Spinner zur Verfügung. Die beiden letztgenannten Teile habe ich erst einmal gar nicht berücksichtigt und auch die Anleitungen waren mir egal. Ich hab einfach mit den Basisteilen (Quadrate, Dreiecke und Trapeze) angefangen frei zu bauen. Und ich sag euch, das ist echt cool. Da ich ja von Berufs wegen als Mathematikdidaktikerin „vorbelastet“ bin, sind mir natürlich gleich viele tolle dreidimensionale geometrische Figuren eingefallen, wie z.B. Würfel, Quader und verschiedene Polyeder. Erst mein Enkel (3 Jahre alt) hat mich darauf gebracht, die Teile platt auszulegen, also auch zweidimensionale Muster und Figuren zu legen.

Ich versuche mal, die Vielfalt der Möglichkeiten des Erforschens der Magnetbauteile zu strukturieren und die mathematischen Kompetenzen, die dabei angesprochen und gefördert werden zuzuordnen.

Freies Bauen und Legen

Sowohl Kita- als auch Grundschulkinder können und sollten natürlich mit den Magnetteilen frei bauen. Das ist super kreativitätsfördernd und hoch motivierend. Jedes Kind kreiert sein eigenes Bauwerk oder Muster ganz nach seinen Interessen. Und ich kann dies als Lernbegleiter gut beobachten. Egal ob dreidimensionale Fantasieformen oder zweidimensionale Legefiguren, jedes Kind hat seine eigenen Ideen und Vorgehensweisen. Und wie viel Mathe steckt dadrin?

Mathematische Kompetenzen:

Förderung von (mathematischer) Kreativität
Erkennen von Vierecken (Quadrate, Trapeze) und Dreiecken und deren Merkmale
Zählen von verbauten, gelegten oder noch benötigten Teilen
Förderung des räumlichen Vorstellungsvermögens
Verwenden mathematischer Begriffe (z.B. rechts, links, oben, unten, Seiten, Kanten, Ecken, Dreieck, Würfel, drei, eckig, …)
Förderung feinmotorischer Kompetenzen und der Auge-Hand-Koordination
…

Bauen nach Vorlagen bzw. Anleitungen

Hierfür könnt ihr zunächst die Beilagen der Packungen nehmen. In meinem Karton sind drei verschiedene Schritt-für-Schritt-Anleitungen für den Bau eines Space Balls enthalten. Das ist schon mal cool. Aber noch cooler sind natürlich die vielen Ideen, die zu diesen Materialien im Internet zu finden sind. Druckt einfach ein paar passende Bilder von geeigneten Bauwerken aus und laminiert sie. Oder aber ihr fotografiert die tollen Bauwerke eurer Kids, druckt die Fotos aus und laminiert auch sie. Dann können andere Kinder diese nachbauen. Tolle Sache! Und ja, ich finde beide Varianten gut und wichtig: 1. Nach einer Schritt-für-Schritt-Anleitung etwas genauso nachbauen und 2. ein Bauwerk von einem Foto nachbauen, denn hier sind manchmal nicht alle Seiten gut zu sehen und man muss aus dem Gesehenen schließen, was nicht zu sehen ist. Und genau dies führt uns zu den Kompetenzen.

Mathematische Kompetenzen:

Fähigkeit der Eins-zu-Eins-Zuordnung
Erkennen von Analogien und Symmetrien
Identifizieren räumlicher Lagebeziehungen
Förderung der visuellen Wahrnehmung
Systematisches Bauen nach Vorgaben und Anleitungen
Abzählen benötigter Teile
Vergleichen der Vorlage mit dem Original

Freies projektartiges Bauen nach Themen

Vor allem in heterogenen Kitagruppen und Schulklassen ist es eine gute Idee nach den freien Bauphasen (vielleicht auch aus der Beobachtung heraus) für alle Kinder ein Thema vorzugeben, das sie nun ganz individuell umsetzen können. Somit werdet ihr dem inklusiven Lernansatz, wonach alle Kinder das gleiche Thema bearbeiten aber jeder auf seiner ganz individuellen Ebene, gerecht. In der Kita und in Klassenstufe 1 und 2 wäre das Thema „Häuser bauen“ zum Beispiel sehr gut geeignet.

Als Arbeitsauftrag würde ich formulieren: „Baue Häuser. Wie viele verschiedene Möglichkeiten findest du?“ Je nach Materialverfügbarkeit und Vorlieben der Kinder können sie allein, zu zweit oder in kleinen Teams zusammenarbeiten. Am Ende kann sogar ein kleiner Ort oder eine lange Häuserzeile aus allen Häusern aufgebaut werden.

In der Auswertungsphase eignen sich Impulse wie:

Aus welchen geometrischen Körpern bestehen eure Häuser? (Oft sind es Würfel, Quader, Pyramiden und Prismen) Hinweis: Die Kinder müssen nicht die geometrischen Fachbegriffe Prisma und Pyramide verwenden. Hier reicht der Alltagsbegriff „Dach“.
Welche Formen werden oft für die unteren Etagen gebraucht? (Zweidimensional gesehen sind es oft Quadrate. Dreidimensional gesehen sind es oft Würfel und Quader)
Welche Formen werden oft für die Dächer gebraucht? (Zweidimensional gesehen sind es oft Dreiecke und Trapeze, manchmal auch Quadrate. Dreidimensional gesehen sind es oft Prismen oder Pyramiden.)
Wie viele Würfel (Quader, Quadrate, Rechtecke, Dreiecke, Trapeze, Prismen, Pyramiden, …) entdeckst du an deinem Haus?
Zähle Flächen, Kanten und Ecken an deinem Haus.
Welche Farben hast du verwendet?
Beschreibe dein Haus ganz genau.
Male dein Haus auf Papier.
Wie viele Möglichkeiten findest du, ein Haus zu bauen?

Mathematische Kompetenzen:

Bauen von dreidimensionalen Körpern aus zweidimensionalen Formen
Erkennen und Unterscheiden von zwei- und dreidimensionalen Formen
Verwenden mathematischer Fachbegriffe bzw. geeigneter Alltagsbegriffe
Zählen geometrischer Formen
Bestimmen der Anzahlen von Flächen, Kanten und Ecken
(Ab)Malen geometrischer Formen
Anbahnen kombinatorischer Denkweisen (verschiedene Möglichkeiten für Häuser finden)

Analog kann für die Klassenstufen 3 bis 6 das Thema „Raumfahrt“ angeboten werden. Hier können die Kinder vor allem mit den Bausätzen von GeoSmart Spacestationen, Ufos, Spacebälle, Raketen, Sterne, Solarspinner und vieles mehr kreieren. Da könnt ihr ja auf der Webseite mal vorbei schauen: www.geosmart.eu

Ja und zum Schluss darf natürlich ein Thema, nein was sage ich da: DAS Thema nicht fehlen, …. Na kommt ihr drauf? Genau „Körpernetze“!!!! Wenn du jetzt denkst, na wie langweilig, dann musst du unbedingt noch weiter lesen.

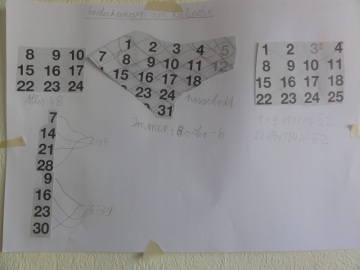
Also das Thema „Körpernetze“ könnt ihr in der Klassenstufe 3 super mit diesen Magnetteilen einführen und in den höheren Klassen immer wieder damit forschen. Der Anfang ist ganz easy: Nachdem ihr zum Beispiel eine würfelförmige Teeschachtel aufgefaltet und zu einem Netz ausgebreitet habt, wissen die Kinder ja nun, was ein Würfelnetz ist. Gebt dann jedem Kind 6 magnetische Quadrate (Ja ich weiß, da braucht man bei 27 Kindern ne ganze Menge und wird arm dabei. Aber viele Kinder haben die Teile zu Hause und bringen sie vielleicht gern mit zur Schule.) und fordert eure Matheforscher auf, ein Würfelnetz zu legen. Das Prüfen durch zusammenbauen ist super einfach und die Kids sehen gleich ob es geklappt hat und ob es ein richtiger Würfel geworden ist. Wenn es ein korrektes Würfelnetz war, dann wieder aufklappen, hinlegen und auf Karopapier aufzeichnen. Jetzt können die Kids weiter forschen und nach weiteren Möglichkeiten für Würfelnetze suchen. Irgendwann kannst du ja zwischendurch mal erwähnen, dass es genau 11 verschiedene Würfelnetze gibt. Mal sehen, wer alle findet!!!

Ein besonderer Impuls für kleine Matheasse wäre: „Lege die Würfelnetze so, dass nach dem Zusammenbauen bei deinem Würfel die gegenüberliegenden Seiten die gleiche Farbe haben.“

So und jetzt das versprochene Highlight: Magische Netze. Im Internet bin ich auf die Idee gestoßen, richtig coole Bauwerke aus manchmal ziemlich komplizierten Netzen zu bauen. Also man kann aus zweidimensionalen Netzen dreidimensionale Körper konstruieren. Und durch den Magnetismus klappt dies ganz magisch wie ein Zaubertrick! Das solltest du unbedingt selbst mal ausprobieren und dann vor der Klasse alle in Staunen versetzen. Vorher können deine Matheforscher ja noch vermuten, was für ein Bauwerk aus dem Netz entstehen wird.

Hier siehst du mal 2 von meinen Experimenten. Hat super geklappt. Man muss einfach in der Mitte vorsichtig hochheben und dann fügt sich das Kunstwerk fast von selbst zusammen. Das klappt wirklich mit nur einer Hand!!!

Mathematische Kompetenzen:

Körpernetze kennen lernen
selbst alle 11 Würfelnetze erforschen und zu Würfeln zusammen bauen
Förderung des räumlichen Vorstellungsvermögens
aus den eigenen Bauwerken Körpernetze aufklappen
selbst Körpernetze entwickeln und zu einem Bauwerk zusammen fügen
Förderung von (mathematischer) Kreativität und von Problemlösefähigkeit
Fähigkeit zum zwei- und dreidimensionalen Denken

Ja und wenn du immer noch nicht genug hast, dann hab ich zum Schluss noch ein paar mathematische (geometrische) Knobeleien für die Klassen 3 bis 6:

Wie viele Würfel kannst du aus 18 Quadraten bauen?
Wie viele Quadrate brauchst du für einen Würfel mit der Kantenlänge 2?
Wie viele Quadrate brauchst du mindestens für einen Quader?
Ich habe zwei Trapeze und zwei Dreiecke, was kann ich daraus bauen?
Baue verschiedene Pyramiden.
Wie kann man eine Kugel / einen Ball bauen? Geht das überhaupt?
Baue einen Tetraeder, Hexaeder und Oktaeder (platonische Körper).

Ich freue mich, wenn du den Beitrag bis hierher gelesen hast und jetzt gleich loslegen möchtest. Ganz viel Spaß dabei!!!

Eure Mandy Fuchs

Grundschule, Matheforscher, Mathematikunterricht, Unterrichtsmaterial

Zettelmathematik – Matheunterricht kann so einfach sein!

2018-08-09 mandyfuchs

Heute habe ich eine geniale Idee für euch zum Schuljahresbeginn, denn in diesem Beitrag erfahrt ihr, wie ihr euren Mathematikunterricht mit einem ganz einfachen Material individuell, handlungsorientiert und dazu noch spielerisch gestalten könnt. Nämlich mit Zetteln aus einer Zettelbox!!! Und ganz nebenbei erwerben bzw. vervollkommnen eure kleinen Matheforscher ihre mathematischen Kompetenzen in vielen Bereichen: Geometrie, Zahlenraum, Einmaleins, Größen und Messen, … um mal nur einiges zu nennen. Und weil es so einfach ist, kann jeder von euch auch ganz spontan echt Klasse Vertretungsstunden aus dem Hut zaubern. Und das von Klasse 1 bis Klasse 6. Wie das geht? Na dann passt auf!

Forscherkartei zur Zettelmathematik — Hier geht`s zur Zettelmathematik

Was brauchst du für Materialien und Lernmittel?

Also wenn es eine richtig coole Forscherstunde werden soll, dann solltest du folgende Sachen vorher bereit halten:

für eine Schulklasse etwa 4 Zettelblöcke (je 500 Blatt)
verschiedene Messgeräte wie z.B. Lineale, Maßband, Zollstock, Waage
noch ein Heftgerät (Klammeraffe)
Kleinmaterial wie z.B. Büroklammern, Muggelsteine, … oder was du sonst noch so im Klassenraum hast
und ja klar Papier, Stifte, Scheren, Klebestreifen

(Noch ein Tipp: Für eine Vertretungsstunde reicht auch nur ein ganz normaler Zettelblock, mehr nicht!!!) Ja und dann kann es losgehen.

Wie kannst du eine Mathestunde zur Zettelmathematik gestalten?

Na also ich bin ja ein Fan von Mathe-Forscherstunden. Aber du kannst auch andere Methoden wählen, wie z.B. eine Lerntheke vorbereiten, Stationen aufbauen oder die Zettelmathematik in den Wochenplan einbauen. Auf jeden Fall sollte es eine offene Organisationsform sein, das heißt dass deine Matheforscher ganz viel selbst entscheiden und auswählen dürfen und somit selbst Verantwortung für ihr Lernen übernehmen. Das ist nicht nur total individuell und differenziert sondern entlastet dich auch enorm. Du schaffst dir somit Freiraum zum Beobachten und individuellen Begleiten von einzelnen Kindern.

Lehrerhandreichung zur Zettelmathematik — Auf diesen Karten erfährst du wie es gehen kann.

Also wie würde ich es machen? Bei mir gibt es in Forscherstunden 3 Abschnitte:

eine Einstiegsphase
eine Forscherphase
eine Auswertungs- und Präsentationsphase.

Hier auch gleich noch ein zeitlicher Tipp: Forschen und Entdecken braucht Zeit, also wäre eine Doppelstunde bzw. ein 90min-Block total günstig.

Einstiegsphase (ca. 10-15min):

Gesprächskreis: in der Mitte ein Zettelblock mit etwa 500 Zetteln
Einstiegsfragen: Was kann man mit den Zetteln erforschen? Oder: Wie viel Mathematik steckt in einem Zettelblock?
jedes Kind bekommt einen Zettel und darf etwas probieren
erste Äußerungen und Ideen der Kinder aufgreifen
gemeinsam erste Forscherfragen zusammentragen und an die Tafel schreiben

Forscherphase (ca. 45 min):

die Kinder mit den Zetteln forschen lassen
dabei vor allem selbst gestellte Forscherfragen oder auch Ideen der Forscherkartei zur Zettelmathematik bearbeiten
auch Stationen durch die Kinder aufbauen lassen
ein Forscherblatt mit den Forscherergebnissen der Kinder erstellen (Einzel-, Partner- oder Gruppenarbeit)

Tipp: Ein Forscherblatt ist ein weißes A4-Blatt, auf dem die Kids ihre Entdeckungen ganz individuell aufschreiben, aufmalen oder aufkleben. Gerade so ein Forscherblatt trägt enorm zum Kompetenzerwerb der SuS bei, denn hier wird das, was sie entdeckt und geforscht haben noch einmal ganz bewusst reflektiert und auf den Punkt gebracht. Wenn du mehr zu Forscherblättern erfahren möchtest, dann kannst du hier nachlesen: Kompetenzorientiert Forscherblätter erstellen

In der Forscherphase besteht die größte Herausforderung für dich, dich zurückzuhalten und die Kinder machen zu lassen. Hab Vertrauen, das klappt! Und sei nicht enttäuscht, wenn deine Kinder nicht auf Anhieb tolle Forscherfragen aufwerfen. Sanfte Impulse von deiner Seite oder durch ausgewählte Forscherkarten der Forscherkartei auf der Grundlage deiner Beobachtungen werden helfen, dass deine Schülerinnen und Schüler immer selbständiger Mathematik erforschen. Glaub mir! Wenn deine Matheforscher noch nicht so an das freie Forschen gewöhnt sind, darfst du sie auch nicht überfordern. Die Gefahr besteht, denn die Zettelmathematik ist einfach zu genial mit all ihren Möglichkeiten!!!!

3. Präsentations- und Auswertungsphase(ca. 30 min):

Ja und am Ende braucht ihr noch genügend Zeit

zum Aufbauen einer kleinen Ausstellung
zur Präsentation der Forscherergebnisse durch die Kinder bzw. Gruppen
zum Vorstellen der Forscherblätter
zur Diskussion, Zusammenfassung und Dokumentation der Forscherergebnisse
für die gemeinsame Reflexion über die „Zettelmathematik“ und das „Matheforschen“

Und wenn ihr habt, dann könnt ihr die Portfolios, Lerntagebücher oder Forscherhefte der Kinder nutzen, in denen sie alles Wichtige dokumentieren können.

So nun bist du sicher total neugierig, welche genialen Forscherfragen und Entdeckungen meine kleinen und größeren Matheforscher aufgeworfen und verfolgt haben. Na dann schau her!

Welche Forscherfragen finden Grundschulkinder spannend?

Wie viele Zettel hat ein Block? Wir schätzen zuerst.
Wie lang ist die Strecke, die man mit allen Zetteln eines Blockes legen kann? Wir schätzen wieder vorher.
Wie hoch wäre ein Turm aus 1 000 000 Zettel?
Was kann man aus Zetteln alles falten oder legen?
Wie oft kann man einen Zettel falten?
Was kann man mit einem Zettel alles anstellen?
Welche Muster kann man aus Zetteln legen?
Kann man mit den Zetteln eines Blockes den Klassenraum auslegen?
Wie viele (Stempel, Büroklammern,….) passen auf ein Blatt?
Wie viele Knüllkugeln passen in ein Glas?
Wie schwer ist ein Block?

Beispiele zur Zettelmathematik

Flächen auslegen und Malaufgaben entdecken

Muster auf Zettel malen

Erkenntnisformen — In diesen Mustern gibt es viel Mathematik zu entdecken!

Schönheitsformen — Hier sieht man viele besonders schöne Muster, die natürlich auch zum Entdecken mathematischer Phänomene einladen.

Viele Dinge aus Zetteln falten

Faltwürfel aus der Zettelbox — Aus immer 6 Zetteln können Würfel entstehen.

Weihnachten kommt auch bald wieder: Der Aurelio Stern ist auch für geübte Hände eine Herausforderung.

Faltfiguren gibt es viele!!! Oft sind es Dinge aus dem Leben (Boote, Flieger, Tiere, …), deshalb Lebensformen.

Mit Zetteln bauen

Zettelmauer — Für dieses Bauwerk braucht es Fingerspitzengefühl. Wie hoch und wie breit ist es? Wie viele Zettel wurden verbaut?

Aus Zetteln gleiche Formen falten und schneiden und daraus Figuren legen

8 Dreiecke — Falte und schneide aus einem Zettel 8 gleiche Dreiecke.

Mit den Zetteln Muster legen

Zettelkreis — Ein Kreismuster aus Zetteln

Zettelmuster — Wie viele Quadrate und Dreiecke sind in diesem Muster versteckt?

Große Vierecke (und andere Formen legen)

Fünflinge (Pentominos) und auch Würfelnetze herstellen

Pentominos (Fünflinge) — Pentominos (und auch Würfelnetze) können mit Klebestreifen ganz einfach hergestellt werden.

Eine Hundertertafel legen

Hunderterfeld — Eine selbst gelegte Hundertertafel lässt sich besonders gut erforschen.

Einen Zettel mit verschiedenen Sachen auslegen

Zettel auslegen — Die Zettel können mit verschiedenen Materialien ausgelegt werden.

Einen Zettel so falten und schneiden, dass man hindurch steigen kann

Durch einen Zettel steigen — Wie muss man falten und schneiden, damit man durch einen Zettel steigen kann?

Selbst ein Tangram erstellen und damit Figuren legen

Knüllkugeln herstellen und damit ein Spiel erfinden

Die meisten Vierecke und Dreiecke falten

Vierecksfaltung — Wer faltet die meisten Vierecke?

Dreiecksfaltung — Wer faltet die meisten Dreiecke?

Quadratzahlen erforschen

Das ist doch alles schon richtig genial, oder? Und deine Matheforscher kriegen das auch hin. Aber Achtung! Nicht alles auf einmal! Manche Ideen der Kinder können auch auf eine der nächsten Mathestunden verschoben werden. Oder du kannst je nach Klassenstufe und Kompetenzen der Kinder bzw. je nach Thema des Mathematikunterrichts oder der Geometriestunde Schwerpunkte setzen oder am besten die Kinder einbeziehen, was zuerst bearbeitet werden soll.

Dann lass uns zum Ende noch einmal zusammenfassen!

Welches mathematische Potenzial steckt in der Zettelmathematik?

Da wären zuerst die Prozessziele sowie mathematischen Denk- und Handlungsweisen zu nennen. Die Zettelmathematik leistet einen Beitrag

beim vertieften Erkennen und „Begreifen“ mathematischer Zusammenhänge
beim weiteren Gewinnen mathematischer und speziell geometrischer Einsichten
zur Förderung feinmotorischer Kompetenzen beim Falten, Schneiden und Auslegen
zur Sprachförderung durch Formulieren von Forscherfragen und durch gemeinsames Kommunizieren
zur Förderung von Kreativität und Problemlösekompetenz
beim Erkennen und Nutzen von Mustern und Strukturen
zur Freude am Umgang mit mathematischen Fragestellungen und Themenbereichen
zur Flexibilität im mathematischen Denken
zur Weiterentwicklung heuristischer Strategien (Probieren, systematisches Vorgehen, Anfertigen von Tabellen und Skizzen)

Und dann sind da noch die mathematischen Inhaltsbereiche, die in der Zettelmathematik „stecken“, nämlich

Zahlen und Operationen (Mengenvorstellungen im Zahlenraum, Zahlenfolgen, Rechenmuster, Hunderterfeld, Malaufgaben des Einmaleins darstellen, …)
Größen und Messen (Längen schätzen und messen, Flächen auslegen, Gewichte ermitteln und vergleichen)
Form und Veränderung, also Geometrie (schneiden, falten, Muster gestalten, ebene Formen legen, dreidimensionale Körper bauen, Bauwerke konstruieren, Kopfgemetrie anwenden, …)

Und zu guter Letzt können auch fächerübergreifende Möglichkeiten genutzt werden, wie z.B. ein Gespräch über den Sinn von Notizzetteln und Notizen oder auch die Verbindung von Themen mit dem Kunstunterricht (z.B. die Zentanglemethode).

Wenn ihr jetzt Lust bekommen habt, euren Mathematikunterricht in der Grundschule mit der Zettelmathematik aufzupeppen, dann könnt ihr gleich loslegen. Holt euch am besten gleich noch heute die Forscherkartei zur Zettelmathematik und los geht’s!

Viel Freude und „verzettelt“ euch nicht!

Eure Mandy Fuchs

Forscherkartei Zettelmathematik 1 — So sehen die Forscherkarten für die Kinder fertig ausgeschnitten und laminiert aus.

Forscherkartei zettelmathematik 2 — Diesmal gibt es insgesamt 18 Forscherkarten mit super vielen Ideen!

Grundschule, Kita

Forschen mit Sudokus

2017-05-14 mandyfuchs Ein Kommentar

Angeregt durch die vielen positiven Kommentare zu meinen Instagrambeiträgen über Sudokus, möchte ich dir dieses Thema heute als „Offenes mathematisches Spiel- und Lernfeld“ vorstellen. Du erinnerst dich sicher noch an die vier Blogbeiträge zu den „Offenen mathematischen Spiel- und Lernfeldern“! Wenn nicht kannst du gern noch einmal nachschauen. Die vier Beiträge standen unter folgenden Schwerpunkten:

Innerhalb von Werkstätten und Ateliers (Auch dazu kannst du den entsprechenden Blogbeitrag noch einmal hier lesen.) – oder aber auch innerhalb der offenen Arbeit in der Kita oder im offenen Unterricht in der Grundschule – haben Kinder stets vielfältige Möglichkeiten des freien Experimentierens, Forschens, Entdeckens sowie des freien Ausdrucks und Gestaltens. Daneben ist es aber ebenso wichtig, ihnen Gelegenheiten zu bieten, sich mit Themen auseinanderzusetzen, auf die sie allein eher nicht kommen würden. Diese Themen sollten jedoch didaktisch so gestaltet werden, dass sie eine gewisse Offenheit in verschiedene Richtungen zulassen.

Sudokus im herkömmlichen Sinne sind bekanntlich nicht so offen, denn hier müssen genau die Zahlen gefunden und ergänzt werden, die noch fehlen, so dass das Sudokurätsel nach den bekannten Regeln richtig gelöst ist. Und dafür gibt es nunmal nur eine richtige Lösung!

Wenn wir jedoch den Kindern keine Zahlen vorgeben, sondern sie anregen, von Beginn an selbst Zahlen nach der bekannten Sudokuregel einzutragen, dann ist ganz schnell eine Offenheit gegeben. Und das schon bei einem 4×4-Sudokufeld. Diese Offenheit kann noch mehr erweitert werden, indem die Kinder nicht nur Zahlen, sondern auch viele andere Dinge nutzen können, z.B. Farbplättchen, Legefiguren, Naturmaterialien, kleine Dinge (z.B. Büroklammern, Spielfiguren, …), Gummibären, Smarties, bunte Würfel (mit und ohne Augenzahlen), Qwirkelsteine, …., der Phantasie sind keine Grenzen gesetzt.

Welches mathematische Potenzial steckt im Forschen und Entdecken mit Sudokus?

Jedes Kind hat die Möglichkeit, eigene Sudokus zu finden.
Es gibt unzählige verschiedene Lösungsmöglichkeiten. (Was schätzt du, wie viele es gibt?)
Verschiedene Vorgehensweisen beim Problemlösen sind möglich: geduldiges Probieren, systematisches Entwickeln, Erzeugen einer neuen Figur aus einer vorherigen, …
Verschiede Lösungsstrategien können angewendet werden (z.B. zeilen- bzw. spaltenweises Vorgehen oder zunächst alle 4 Dinge einer Sorte im Feld verteilen und dann weiter Auffüllen).
Die Kinder können eigene Forscherfragen zu Sudokus finden und lösen.
Sudokus leisten einen Beitrag zur Förderung des schlussfolgernden und logischen Denkens und zur Förderung von Problemlösekompetenzen.
Kleine Matheforscher können Muster und Strukturen erkennen und nutzen.
Forschen mit Sudokus beinhaltet die Themenfelder Raum & Form sowie den Bereich der Kombinatorik.
Es kann ein „Super-Sudoku“ gefunden werden, in dem die Regel auch in den beiden Diagonalen, in den vier Ecken und im inneren Viererfeld gilt.

Welche Materialien und Lernmittel brauchen kleine Matheforscher für das Forschen mit Sudokus?

Rätselhefte mit Sudokus und Sudoku-Spiele für Kinder (vielfach im Handel erhältlich)
Vorlagen mit 4 mal 4-Sudokufeldern (z.B. zu finden bei Lehrermarktplatz)
16 Farbenplättchen (z.B. 4 rote, 4 gelbe, 4 blaue, 4 grüne Plättchen), 16 Farbwürfel oder 16 andere Gegenstände (z.B. 4 Kastanien, 4 kleine Zapfen, 4 Haselnüsse, 4 Eicheln), Ziffernplättchen, …

Wie kann der Ablauf eines offenen Forscherangebotes in der Kita oder einer Forscherstunde in der Grundschule zu Sudokus gestaltet werden?

Einstiegsphase:

über individuelle Vorerfahrungen der Kinder mit Sudokus sprechen
Kinder können mitgebrachte Sudoku-Rätsel und Spiele zeigen und damit evtl. gemeinsam spielen
Besonderheiten und Lösungsregeln beim Sudoku gemeinsam zusammentragen (Ziel beim Sudoku ist, ein 4 x 4-Feld mit Farben (oder Symbolen) so zu füllen, dass jede Farbe (oder jedes Symbol) in einer Zeile, in einer Spalte und in einem Viererfeld nur einmal vorkommt.)
die Struktur eines leeren 4 x 4 Sudokufeldes erkunden, dabei wesentliche Begriffe wie z.B. „Zeile“, „Spalte“ und „Viererfeld“ nutzen und deren Anzahlen bestimmen
sinnvoll ist, ein Sudoku (an einer Tafel o. ä.) beispielhaft mit allen Kindern zu besprechen und gemeinsam zu lösen, dafür können Farben oder Symbole verwendet werden
Hinweis: Im Unterschied zu Sudokus in Rätselheften sollten keine Angaben vorgegeben werden. Die Kinder stellen von Anfang an ihre eigenen Sudokus her.

Forscherphase:

Sudokus mit vier verschiedenen Farben (oder anderen Dingen) legen und verschiedene Möglichkeiten für 4 x 4-Sudoku-Quadrate finden, dabei die Sudoku-Regel einhalten
für die Darstellung und das Dokumentieren gefundener Lösungen können vorbereitete Blätter genutzt werden (z.B. zu finden bei Lehrermarktplatz)
gefundenen Lösungen können aufgemalt werden
während des Forschens die Kinder zum Aufwerfen neugieriger und interessanter Fragen anregen
Tipp: Alternativ zu den Farben können andere Materialien (z.B. Spielfiguren, Knöpfe, Deko-Streufiguren, …) oder auch bereits Zahlen und Buchstaben oder andere Symbole verwendet werden.

Präsentations- und Auswertungsphase:

Zusammentragen aller Forscherergebnisse
Gespräch über die Entdeckungen der Kinder

Welche Fragen und Impulse eignen sich zur Begleitung der Kinder beim Forschen?

Wie viele Zeilen, Spalten und Viererfelder siehst du?
Ich sehe du verteilst erst alle 4 roten Plättchen. Das ist eine gute Strategie!
Wie viele verschiedene Lösungen findest du (findet ihr) zusammen?
Vergleicht eure Lösungen. Was fällt euch auf?
Wie kann man aus einem vorhandenen Sudoku ein neues Sudoku legen? Hast du dafür einen Trick?
Gibt es (Entdeckst du) ein besonders schönes Sudoku-Muster?

Welche weiteren möglichen Entdeckungen gibt es?

Die Idee mit den Würfeln aufgreifend ergibt eine weitere sehr anspruchsvolle Möglichkeit: Sudokus dreidimensional in die Höhe zu bauen. Hierbei können die Kinder wiederum verschiedene Lösungsstrategien anwenden. Eine sehr effektive Strategie ist z.B. die Farben geschickt zu tauschen, d.h. auf jeden grünen Würfel kommt ein gelber Würfel, auf jeden roten Würfel kommt ein blauer und umgekehrt. Diese Strategie wird in den nächsten Ebenen mit den anderen Farben so fortgesetzt. Bei diesem oben abgebildeten Sudoku ist zudem sehr schön zu verfolgen, wie sich das Muster verändert: Die „Schrägen“ mit 3 gelben, 3 grünen, 3 roten und 3 blauen Würfeln verändern ihre Lagen nach einer bestimmten Regel (In der zweiten Ebene tauschen grün und gelb sowie rot und blau. In der dritten Ebene drehen sich die „Schrägen“ im Uhrzeigersinn. In der vierten Ebene tauschen wieder gelb und grün sowie rot und blau.).

So, ich denke das reicht mit den Ideen, sonst bleibt ja für euch und eure kleinen Matheforscher nichts mehr zum Erforschen übrig.

Na dann könnt ihr loslegen! Viel Erfolg beim Sudokuforschen wünscht euch

Mandy Fuchs

Eltern, Grundschule, Kita, Mathematik im Spiel

Spiele für die Mathewerkstatt

2017-04-05 mandyfuchs Hinterlasse einen Kommentar

Im Moment entstehen ja gerade die Blogbeiträge zur Einrichtung einer Mathewerkstatt (sowohl in Kitas als auch in Grundschulen). Für alle, die es jedoch nicht erwarten können, möchte ich heute schon ein paar sehr geeignete Spiele bzw. Spielmaterialien vorstellen, die nicht nur jede Mathewerkstatt bereichern, sondern auch für kleine Matheforscher zu Hause total spannend sein können.

Für kleine Matheforscher in Windeln aber auch für größere bis etwa 7 Jahre empfehle ich die bunten Bären.

Diese Bären gibt es in drei verschiedenen Größen (und Gewichten), so dass als erstes schon ein genialer Sprechanlass gegeben ist: „Das sind ja immer kleine Bärenfamilien!“ … und schon können die Kinder in Rollenspiele „abtauchen“. Aber nicht nur das! Die 80 bunten Bären (in den vier Farben rot, gelb, grün und blau) sind ideal zur Förderung von frühen mathematischen Kompetenzen geeignet:

immer wieder zählen,
sortieren nach Farben, Größen oder Familien,
nach bestimmten Merkmalen ordnen oder auch
farbige Musterreihen nach eigenen und/oder vorgegebenen Regeln können aufgebaut werden.

Sogar für Sudokus sind sie geeignet!

Die proportional gewichteten Bärenfiguren eigenen sich auch perfekt zum Abwiegen auf einer Spielbalkenwaage. Und dabei können die größeren Matheforscher z.B. erkennen: Zwei Babybären sind genauso schwer wie eine Mamabärin und zwei Mamabären sind so schwer wie ein Papabär, also sind vier Babybären so schwer wie ein Papabär. Genial, oder?

Mein zweiter Tipp sind die bunten Kettenglieder.

Diese empfehle ich für Matheforscher im Alter von etwa 4 bis 10 Jahren. Denn auch sie bieten eine Reihe genialer Möglichkeiten für das Erforschen mathematischer Beziehungen. Ein ausführlich erprobtes offenes Spiel- und Lernfeld zu den bunten Ketten findet ihr im Buch: „Alle Kinder sind Matheforscher“. Hier aber mal ein paar Ideen zusammengefasst:

Stärkung der Feinmotorik: durch das Zusammenfügen der einzelnen Kettenglieder,
Musterketten bilden: durch das Zusammenstecken der Kettenglieder nach ganz bestimmten Merkmalen entstehen logische Reihenfolgen, die die Kinder erkennen, beschreiben, nachbauen und selbst bauen können,
Messen: die Kinder können z.B. 10er- oder 20er-Ketten herstellen und mit diesen Ketten Gegenstände im Raum oder Abstände und Wege ausmessen (z.B.: Der Tisch ist drei 10er-Ketten breit.),
Schätzen: die Kinder werden angeregt zu schätzen, wie lang ihre Ketten sind und wie viele Kettenglieder sie gebraucht haben (Tipp: Der „Renner“ bei meinen Kindern war und ist immer wieder das Erforschen, wie lang wohl die Kette wird, wenn alle (500!!!) Kettenglieder aus der Box zusammengesteckt werden.)
Rechnen: Ganz automatisch und fast nebenbei beginnen die Kinder Rechenaufgaben zu ihren Ketten zu bilden. Ein Tipp für Matheforscher im 2. Schuljahr: Die Ketten eignen sich super, um die Malfolgen und ihre Zusammenhänge darzustellen. Probiert es selbst aus und stellt die 2er-Folge (immer zwei gelb – zwei blau), die 4er-Folge (immer vier gelb – vier blau) und die 8er-Folge (immer acht gelb – aucht blau) her und hängt sie nebeneinander! Nicht schlecht, oder?

Und mein letzter Tipp für heute: BLOKUS

Empfohlen wird das Spiel ab 7 Jahre. Mit interessierten Matheforschern kann man es sicher auch schon früher spielen. Es ist ein Strategiespiel (auch für die ganze Familie) mit unzähligen Spielkombinationen. Jeder Spieler wählt eine Farbe und muss die Steine dieser Farbe von den Ecken des Spielbretts ausgehend ablegen. Alle gleichfarbigen Steine müssen dabei eine direkte Verbindung haben. Sie dürfen sich immer nur an den Ecken berühren – nie an den Seiten. Das Spiel ist zu Ende, wenn ein Spieler alle seine Steine abgelegt hat oder kein Spieler mehr ablegen kann. Wer die wenigsten Quadrate übrig hat, hat gewonnen! Das Strategiespiel fördert neben feinmotorischen Kompetenzen das logische Kombinieren, die Konzentration, das analytische und strategisches Denken sowie das räumliche Vorstellungsvermögen. Zum Spiel gehören ein quadratisches Spielbrett mit 400 Feldern, 84 Steine (je 21 Steine in vier Farben). Jeder der 21 Steine einer Farbe hat eine andere Form. Es gibt einen Stein mit 1 Quadrat, einen Stein mit 2 Quadraten, zwei Steine mit 3 Quadraten, fünf Steine mit 4 Quadraten und zwölf Steine mit 5 Quadraten. Somit ist das Material auch super zum weiteren Matheforschen (auch mal allein) geeignet. Zum Beispiel kann man versuchen, das Spielfeld möglichst lückenlos mit den Spielsteinen auszulegen (zu parkettieren). Dabei können kleine Matheforscher auch wieder Muster und Tricks entdecken.

So das wars für heute. Wer nicht bis zum nächsten Spieletipp warten möchte, der kann schon mal hier auf meiner Webseite (Tipps für Spiele) vorbei schauen.

Bis bald, ach ja und wer auch ein tolles mathematisches Spiel(material) empfehlen möchte, kann mir diesen Tipp gern zuschicken.

Mandy Fuchs

Alltagsmathematik, Forscherblätter, Grundschule, Kita

Individuelles Lernen mit Forscherblättern

2017-01-31 mandyfuchs Hinterlasse einen Kommentar

Immer wenn meine kleinen Matheforscher die mathematische Welt mithilfe von Alltagsmaterialien erforschen, rege ich sie an, Forscherblätter zu ihren Entdeckungen zu gestalten. Darüber habe ich euch hier im Blog schon des Öfteren berichtet. Immer wieder werde ich gefragt, was denn überhaupt solche Forscherblätter sind und wie die Kinder sie erstellen. Darum soll es heute gehen.

Aber zunächst frage ich dich als Lernbegleiterin einer Schulklasse oder einer Kindergartengruppe oder auch als Lernbegleiter deines eigenen Kindes heute noch einmal: Was meinst du, wie funktioniert lernen? Wie lernst du am besten? Was für ein Lerntyp bist du? Ich zum Beispiel bin ein sehr strukturierter Typ, ich liebe systematische Übersichten. Am besten, wenn ich sie mir selbst und allein erarbeite. Aber ich probiere auch gern mit anderen etwas aus. Und du? Brauchst du Bilder, musst du es selbst tun oder brauchst du die Diskussion mit anderen? Probierst du auch gern etwas aus oder bist du eher ein kreativer Chaot, der intuitiv vorgeht? Wie auch immer! Alles hat seine Berechtigung und jedes Vorgehen ist wertvoll! Ja und so wie wir Erwachsenen ganz unterschiedliche und individuelle Lernwege beschreiten, tun es auch unsere Kinder … wenn man sie lässt! Sie haben vielfältige Ideen, gehen unterschiedlich vor, lernen in ihrem eigenen Tempo, gern auch mit anderen und nutzen ihre eigenen und ganz intuitiven Theorien.

Ursprünglich ist Lernen durch folgende noch immer geltenden Merkmale geprägt:

Der Antrieb zur Nachahmung: Kinder beobachten und machen nach, sie brauchen also Vorbilder an denen sie sich orientieren können (Rolle von Eltern und von pädagogischen Fachkräften).
Der unaufschiebbare Drang zur Selbständigkeit: Kinder fühlen sich unwohl und missverstanden, wenn ihnen alles abgenommen und erklärt wird. Sie wollen nicht in eine passive und unmotivierte Konsumentenrolle gedrängt werden.
Die Zurückweisung von Belehrungen: Kinder wollen Selbsterfahrungen sammeln und Selbstwirksamkeit erleben, sie brauchen deshalb Aufgaben, an denen sie wachsen können.
Körpererfahrungen: Kinder wollen mit allen Sinnen lernen, die Welt „begreifen“ und ihren Bewegungsdrang ausleben.
Die soziale Dimension von Lernen und Bildung: Niemand kann in Isolation lernen, Kinder brauchen Bindungspersonen und Gemeinschaften, in denen sie sich wohl und aufgehoben fühlen, denn ohne Bindung kann keine Bildung stattfinden.

Ausgangspunkt moderner Lernkonzepte, die aktuell in der Pädagogik diskutiert werden, ist zudem die Vorstellung, dass jedes Kind seine Welt selbst erobert. Das meint, der Lernende eignet sich Lerngegenstände aktiv auf der Grundlage bereits vorhandener individueller Handlungs- und Denkstrukturen sowie bisheriger Erfahrungen an. Sowohl das entdeckende Lernen als auch eine angemessene Lernbegleitung spielen hierbei eine entscheidende Rolle. Diese – man nennt sie ko-konstruktivistische – Sichtweise betont neben der Eigenständigkeit des Kindes ebenso seine Neugier und seinen Forscherdrang von Natur aus. Jedes Kind möchte lernen und seine Umwelt erforschen, um seinem Bedürfnis nach Erleben von Kompetenz und Wirksamkeit, nach Autonomie und Selbstbestimmung nachzugehen. Das Lernen liegt demnach in der Verantwortung des Kindes, welches sich als kompetenter Akteur von Geburt an autonom mit seiner Umwelt auseinandersetzt. Lernen ist also ein Prozess der Selbstorganisation, wobei insbesondere die Stärken und individuellen Gaben jedes Menschen in den Mittelpunkt rücken. Lernen ist demzufolge immer individuell und von Mensch zu Mensch verschieden.

„Jedes Kind zeichnet sich durch eine eigene Persönlichkeit aus. Es beschreitet individuelle Wege, um ein Verständnis für seine Umwelt aufzubauen und Dingen eine Bedeutung, einen Sinn zu verleihen. Die pädagogisch Handelnden werden dem durch die Individualisierung von Bildungsprozessen bei der gemeinsamen Gestaltung der Interaktion gerecht.“ (Fthenakis u.a. 2009, S. 30)

In meinen Projekten biete ich zum Beispiel meinen kleinen Matheforschern anregende Lernumgebungen. Oft sind es Alltagsmaterialien (z.B. Gummibären, Wattestäbchen, Centstücke, Wäscheklammern, Deckel von Getränkeflaschen, …) mit einem hohen mathematischen Potenzial zum Zählen, Sortieren, Strukturieren, Rechnen, Problemlösen, Knobeln, kreativen Gestalten, Experimentieren und Entdecken. Ich rege die Kinder an, diese Materialien selbst zu erforschen und eigene Forscherfragen zu finden. Wenn sie dann diesen selbst gestellten Forscherfragen auf den Grund gehen, haben sie die Möglichkeit, über Ziele, Inhalte, Tempo, Vorgehensweisen und Lernformen individuell zu bestimmen. Kleine Matheforscher lernen so stets selbstbestimmt, interessenorientiert, eigenverant-wortlich, selbstorganisiert, sehr differenziert und individuell. Sie lernen nachhaltig und mit viel Freude. Ihre Forscherergebnisse stellen sie oft auf einem Forscherblatt zusammen, welches sie in der Auswertungsphase dann auch präsentieren. Somit haben wir eine gute Grundlage, um miteinander ins Gespräch zu kommen und über geniale Ideen oder aber auch fehleranfällige Strategien zu diskutieren.

Ich werde also immer wieder gefragt, wie solche Forscherblätter aussehen und wie meine Matheforscher sie anfertigen? Meine Antwort lautet: Ganz individuell! Damit ihr liebe Blogleser und Blogleserinnen eine Vorstellung von solchen Forscherblättern bekommt, stelle ich euch heute einige vor.

Zwei Beispiele für Forscherblätter von Vorschulkindern

Im Sommer haben wir uns mit dem Erforschen von Eiskugelmöglichkeiten beschäftigt. Herauszufinden waren viele (oder sogar auch alle) Möglichkeiten, die es gibt, wenn man drei Kugeln Eis kauft und es beim Eismann genau drei Sorten, z.B. Schoko, Erdbeere und Vanille gibt. Das sind die Forscherblätter von Lara, Leonardo und Paul:

Immer wieder erforschen meine Kinder gern den Inhalt von Smartiespackungen. Hierzu stelle ich euch demnächst auch die Forscherkartei (wie die Forscherkartei zur Gummibärenmathematik) zur Verfügung. Hier seht ihr wie Lanis und Leonardo, zwei 6-jährige Matheforscher, die Farbverteilung der Smarties auf ihrem Forscherblatt in einem Schaubild dargestellt und miteinander verglichen haben:

Vier Beispiele für Forscherblätter von Grundschulkindern

Zwei Drittklässler haben hier ihre Entdeckungen am Kalender auf einem Forscherblatt dargestellt:

Als wir uns mit Fermiaufgaben beschäftigt haben, hatte Helen (4.Klasse) die Idee, zu diesem Aufgabentyp ein Infoblatt für andere Kinder am Computer zu erstellen. Dies setzte sie total eigenständig in nur einer Forscherstunde am Klassen-PC um. Klicke hier, um es dir anzusehen: fermi

Manchmal enthält ein Forscherblatt auch „nur“ die übersichtliche Darstellung eines Rechenweges oder verschiedener Lösungsmöglichkeiten wie hier, bei einer Fußballknobelei:

Jannis (3. Klasse) liebt Zahlen- und Rechentricks und bringt diese oft mit in die Schule zum Matheunterricht. Einmal durfte er nicht nur den Trick vorführen und seine Klassenkameraden beeindrucken, sondern auch ein Forscherblatt dazu erstellen. Leider behielt er es wie ein wahrer Rechenkünstler für sich, wie genau der Trick funktioniert! Zum Ansehen seines Forscherblattes klicke hier: jannis-zahlentrick

So ich glaube eins ist ganz deutlich geworden: Für das Erstellen von Forscherblättern gibt es kein Rezept und keine Anleitung. Unsere Aufgabe als Erwachsene ist es, jedes Kind, also jeden kleinen Weltentdecker und Matheforscher, je nach subjektivem Lerntyp ganz individuell zu begleiten und dabei seine spezifischen Bedürfnisse, Stärken und Ideen zu berücksichtigen. Bei einem Forscherblatt gibt es eigentlich auch kein „richtig“ oder „falsch“. Und das wichtigste: Jedes Forscherblatt ist einmalig! So wie jedes Kind!

Ich wünsche euch viele tolle Augenblicke und AHA-Erlebnisse, wenn eure Kids Forscherblätter erstellen!

Bis bald Mandy Fuchs

Alltagsmathematik, Eltern, Grundschule, Kita

Gummibärenmathematik

2017-01-22 mandyfuchs 4 Kommentare

Du nascht so gerne Gummibären? Zugegeben ich mag sie auch sehr gern, vor allem deshalb, weil man mit ihnen so viel und so genial Mathematik erforschen kann. Glaubst du nicht? Na was meinst du, wie viele Gummibären sind in einer normalen Gummibärentüte? Und wie viele Gummibären gibt es von jeder Farbe? Ist das in allen Tüten gleich? Wie lang ist wohl die Strecke, wenn du alle Gummibären einer Tüte aneinander legst? Und wie viele Gummibären sind so schwer wie ein Kilogramm? Und in deinen Mund, wie viele Gummibären passen da wohl rein? …

Das sind nur einige der Fragen die sich meine kleinen Matheforscher aus der Grundschule und auch aus dem Kindergarten gestellt haben. Und jedes Mal bin ich immer wieder aufs Neue fasziniert und begeistert, was ihnen alles zu den Gummibären einfällt. Aber nicht nur die Fragen sind spannend, sondern auch ihre eigenen Ideen zur Beantwortung. Die Kinder stellen sehr gern selbst zu Beginn Vermutungen auf. Sie hierbei zu beobachten und zum Beispiel ihre Schätzstrategien zu hinterfragen, kann so wertvoll für die weitere Forscherbegleitung und für die Entwicklung mathematischer Kompetenzen sein.

Und genau davon stecken so viele in nur einer Tüte Gummibären. Du kannst es dir noch immer nicht so richtig vorstellen? Dann schau mal hier, das sind die Mathematischen Inhaltsbereiche:

Zahlen und Operationen (Gummibärenanzahlen schätzen, sie zählen, vergleichen und gleichmäßig verteilen, damit rechnen, …)
Größen und Messen (Gummibärenschlangen messen, Gewichte von Bären ermitteln, Preis bestimmen, …)
Form und Veränderung (Muster legen und fortsetzen, Symmetrien erkennen, …)
Stochastik (Daten erfassen und in Strichlisten, Tabellen oder Diagrammen und Schaubildern darstellen, über Wahrscheinlichkeiten diskutieren, …).

Aber auch eine Menge mathematischer Prozessziele sowie mathematische Denk- und Handlungsweisen kannst du mit der Gummibärenmathematik fördern, denn sie leistet einen Beitrag

zur Förderung feinmotorischer Kompetenzen beim Legen der Gummibären,
zur Sprachförderung durch Formulieren von Forscherfragen, durch gemeinsames Kommunizieren und Präsentieren,
zur Förderung von Kreativität und Problemlösekompetenz sowie
zum Erkennen und Nutzen von Mustern und Strukturen.

Und all das ist nicht nur in der Grundschule und im Kindergarten möglich, sondern auch zu Hause. Denn auch Eltern können mit ihren Kindern Gummibären mathematisch erforschen. Das Naschen darf dabei natürlich in keinem Fall zu kurz kommen!

So, ich möchte hier heute aber gar nicht so viel mehr verraten, denn ich habe alle meine gemeinsam mit vielen Kindern und Lernbegleitern erprobten Erfahrungen zur Gummibärenmathematik in einer Forscherkartei zusammengefasst. Diese ist ab sofort bei www.lehrermarktplatz erhältlich. Es gibt dort eine Forscherkartei für kleine Matheforscher in der Grundschule, und es gibt zudem auch Forscherkarten mit Impulsen für kleine Matheforscher und ihre Lernbegleiter im Kindergarten. Alles didaktisch und methodisch aufbereitet und trotzdem mit vielen Möglichkeiten zum freien Forschen und Experimentieren.

Es ist ganz einfach: Die Seiten ausdrucken, laminieren, 8 bzw. 10 Karten zuschneiden und dann kannst du auch schon gemeinsam mit deinen Matheforschern loslegen. Alles was ihr braucht, steht auf den Forscherkarten drauf. Und diese sind immer wieder verwendbar, also kein Verbrauchsmaterial. Du musst auch keine anderen Arbeitsblätter kopieren.

Um zwei Dinge würde ich dich sehr gern bitten:

Wenn du die Kartei mit deinen Kindern ausprobiert hast, wäre es für mich sehr hilfreich, wenn du mir ein Feedback gibst (kontakt@mandyfuchs.de). Was hat super gut funktioniert und was eher nicht? Welche Hinweise hast du zur Gestaltung, zum Layout, zu den Inhalten, usw.? Denn die Gummibärenmathematik ist der allererste Prototyp einer Forscherkartei, die wachsen soll. Geplant sind für beide Bereiche (Kita und Grundschule) viele weitere Themen, die du sammeln kannst. Und eigentlich entstehen so jeweils zwei Karteisammlungen: eine immer für die Lernbegleiter (die Erzieherinnen und Erzieher in der Kita und die Grundschullehrerinnen und –lehrer) und die andere natürlich für die kleinen Matheforscher (die Kinder in den Kitas und in den Grundschulen).
Wenn dir die Forscherkartei so gut gefällt, dass du sie weiter empfehlen möchtest, dann solltest du ausschließlich auf www.lehrermarktplatz.de verweisen. Bitte vervielfältige sie nicht einfach für deine Kolleginnen und Kollegen! Dies ist ausdrücklich nicht gestattet!

Also ich bin schon gespannt, wie sie dir gefällt und freue mich von dir zu hören. Viel Freude bei der Gummibärenmathematik, beim Forschen und Naschen!

Beste Grüße, Mandy Fuchs

Alltagsmathematik, Eltern, Grundschule, Kita

Durch die „mathema-tische Brille“ geschaut

2017-01-18 mandyfuchs Hinterlasse einen Kommentar

Sei ehrlich, woran denkst du, wenn du ans Lernen denkst? Und um es konkret zu machen, ans Lernen von Mathematik? Was für Bilder kommen da in deinen Kopf? Ist es eine verstaubte Schultafel mit viel zu vielen Rechenaufgaben? Oder ist es ein Mathebuch mit endlos erscheinenden Rechentürmchen? Ist es der pralle (oft blaue) Schnellhefter deines Kindes mit zahllosen Kopiervorlagen? Sind es die Arbeitsblätter in der Vorschulgruppe, auf denen die Kinder Mengen erfassen oder Anzahlen ausmalen sollen?

Ja ich gebe zu, lange Zeit dachten wir (und ich meine uns LehrerInnen, ErzieherInnen, Pädagogen und Eltern), dass Mathematiklernen genauso funktioniert: Ein Erwachsener „hat da schon mal was vorbereitet“, er „vermittelt“ es an die Kinder und hofft, dass seine „mathematischen Rezepte“ gelingen und bei den Kids gut ankommen. Funktioniert auch in gewisser Weise, wenn wir Kindern das Denken abnehmen wollen, sie mit unseren Ideen überschütten, sie zum Auswendiglernen und Widerkäuen zwingen. Und uns dann wundern, dass sie es eigentlich gar nicht verstanden haben, Gelerntes nicht anwenden können bzw. ihr Interesse am Forschen und Entdecken verlieren, weil sie ja gelernt haben abzuwarten. Abzuwarten bis jemand kommt und es ihnen erklärt. Ist irgendwann auch viel bequemer als selbst kreativ zu werden.

Nun fragst du dich sicher: Ja wie funktioniert Mathematiklernen denn dann?

Ich lade dich ein, es selbst herauszufinden, mit einem kleinen Experiment: Setz doch mal ganz bewusst deine „mathematische Brille“ auf. Schau dich dort, wo du gerade sitzt und diesen Beitrag liest, um. Was kannst du entdecken? Ich bin sicher, dass du viele Dinge siehst, die eine ganze Menge mit Mathematik zu tun haben. Denn Mathematik steckt überall in unserem Alltag. Schau dir doch mal deine Fenster genauer an. Sieh mal auf den Fußboden. Was ist mit dem Tisch und dem Stuhl an bzw. auf dem du gerade sitzt? Ja genau: Mathematik hat sehr viel mit Mustern und Strukturen, mit Formen und Figuren zu tun. Das ist das eigentliche Wesen der Mathematik. Und das gilt es zu entdecken. Man hat dabei immer eine Menge zu messen, zu zählen. zu rechnen, zu vergleichen und zu ordnen. Und glaube mir, es macht nicht nur viel mehr Freude gemeinsam mit den Kindern auf mathematische Erkundungstouren zu gehen, sondern das Lernen ist so auch viel nachhaltiger als wenn du ihnen ausschließlich Schulbuchaufgaben, Kopiervorlagen oder Arbeitsblätter zum Üben gibst. Und das gilt für die Schule, für die Kita und für zu Hause. Denn „Alle Kinder sind Matheforscher“! Hier findest du noch viele weitere Beispiele zum Erforschen der mathematischen Welt gemeinsam mit deinen Kindern.

Zurück zu unserem Experiment. Schau durch deine „mathematische Brille“ zum Beispiel mal hier:

Ich sitze gerade hier an meinem Laptop und schaue aus dem Fenster. Was kann ich an meinem Fenster entdecken? Genau: Es sind viele kleine Rechtecke, sie sind in fünf Reihen von links nach rechts und in sechs Reihen von oben nach unten angeordnet, es gibt genau zwei gleichgroße Hälften und eigentlich könnte man mit meinem Fenster wunderbar die Malfolge der 3 entdecken, üben und sogar auswendig lernen. Siehst du es? (Vielleicht kannst du deine Kinder ja anregen kleine Klebezettel mit Zahlen oder Aufgaben an das Fenster anzubringen.) Und ja du hast dich gerade nicht verlesen. Ich bin nicht dagegen etwas auswendig zu lernen, wie du vielleicht weiter oben im Text vermutet hast. Die mathematischen Grundaufgaben des kleinen Einspluseins und Einmaleins müssen die Kinder ganz einfach gedächtnismäßig beherrschen. Sie gehören zum mathematischen Fundament dazu, auf dem man dann nach und nach sein individuelles MATHEHAUS aufbauen kann.

Da habe ich gleich auch noch zwei Spieletipps dazu:

Und noch ein zweites Beispiel, das hier ist mein Fußboden:

Der Fotoausschnitt zeigt z.B. ein vier-mal-vier-Quadrat … Bist du eigentlich schon mal über deinen Fliesenfußboden gehüpft, hast dabei einen Zahlenreim oder ein Hüpfspiel erfunden? Nein? Na probier es mal oder lass es deine Kinder tun. Du wirst staunen, wie kreativ sie dabei sind.

So, jetzt kannst du die „mathematische Brille“ wieder absetzen. Die brauchst du nun nicht mehr, denn ich bin mir sicher, dass du ab jetzt viel mehr mathematische Phänomene, Muster, Zahlen und Dinge in deinem Alltag erkennst, als vor dem kleinen Experiment. Stimmts? Dann lade doch nun deine Kinder zu einer mathematischen Erkundungstour ein, egal ob in der Kita, auf dem Schulhof, im Supermarkt oder zu Hause! Mathematik ist überall! Und ich freue mich, wenn du sie weiter gemeinsam mit mir entdecken möchtest. Viele Inspirationen dafür bekommst du auf meinen Profilen als „Matheforscher“ bei Instagram und Pinterest! Vielleicht sehen wir uns dort wieder.

Bis dahin wünsche ich dir viel Freude am Matheforschen!

Mandy Fuchs

Alltagsmathematik, Eltern, Grundschule, Kita

Eine Zahlenforscher-Reise ins Jahr 2017

2017-01-03 mandyfuchs 4 Kommentare

Wir Menschen haben uns die Zahlen in unser Leben herein geholt und seit es sie gibt, sind wir fasziniert von ihnen. Egal ob Uhrzeiten, Termine, Entfernungen, Gewichte, Preise, Einkünfte, Fußballergebnisse, Rekorde oder Geheimzahlen, Zahlen sind aus unserem Leben einfach nicht wegzudenken. Sogar Glücks-, Pech- und Lieblingszahlen beeinflussen so manche unserer Handlungen im täglichen Miteinander. Grund genug, sich immer mal wieder etwas genauer mit ihnen zu beschäftigen. Zu Beginn eines neuen Jahres bietet es sich an, die neue Jahreszahl etwas genauer unter die Lupe zu nehmen: 2017! Dazu möchte ich dich und deine Matheforscher heute gern einladen.

Zunächst einmal könnt ihr doch einfach (ganz unmathematisch) überlegen, was die neue Jahreszahl 2017 so besonders für euch macht? Warum ist 2017 vielleicht bedeutsam für euch? Gibt es ein ganz spezielles Jubiläum in eurer Familie oder innerhalb der Einrichtung in diesem Jahr zu feiern? Oder wird eines deiner Kinder zufällig am 20.1. sieben Jahre alt? Mir erzählte gerade eine Mutter, dass ihre Tochter 20 Jahre alt ist und am 1.7. heiraten wird. Welche persönlichen, familiären oder beruflichen Veränderungen stehen in diesem Jahr bei euch an (Einschulung, Umzug, Geburt eines Kindes, …)? Dieser Austausch kann schon mal sehr spannend für alle Beteiligten sein und zu anregenden Gesprächen führen.

Anschließend kannst du speziell zur Zahl 2017 ein mathematisches „Brainstorming“ durchführen. Und das tolle ist, jeder kann mitmachen: kleine und große Matheforscher. Was fällt dir alles zur Zahl 2017 ein?

2017:

ist eine ungerade Zahl,
besteht aus den Ziffern 2, 0, 1, 7,
hat sieben Einer, einen Zehner, null Hunderter und zwei Tausender,
ist gleich: 2000+10+7,
ist der Nachfolger von 2016 und der Vorgänger von 2018,
hat die Quersumme 10 (2+0+1+7=10)
ist eine Primzahl,
wird in römischen Zahlzeichen so geschrieben: MMXVII
wird im dualen Zahlsystem so geschrieben: 11111100001 (Binärzahl)
…

Je nach den besonderen Interesse der kleinen und größeren Matheforscher können dann einzelne Teilaspekte nochmal besonders herausgegriffen und thematisiert werden. So könnte man die Kinder anregen, zur Zahl 2017 viele Rechenaufgaben zu bilden und zu rechnen, ganz egal ob die Zahl Rechenzahl oder Ergebnis einer Aufgabe ist.

Max (3. Klasse) hatte diese Ideen:

2017 + 1 2017 – 1 2017 · 1

2017 + 10 2017 – 10 2017 · 10

2017 + 100 2017 – 100 2017 · 100

2017 + 1000 2017 – 1000 2017 · 1000

Lisa (4. Klasse) machte es so:

2017= __ +__

2017= __ – __

2017= __ · __

2017= __ : __

Helen (6.Klasse) beschäftigt sich zurzeit gerade ausführlich mit Primzahlen. Das Sieb des Eratosthenes findet sie besonders toll. Sie weiß bereits aus der Grundschule, dass eine Zahl dann eine Primzahl ist, wenn sie größer als 1 und nur durch 1 und durch sich selbst teilbar ist. Sie erforschte, dass 2017 die 306. Primzahl ist. Erst in 10 Jahren wird eine Jahreszahl wieder eine Primzahl sein, nämlich 2027 und dann ist Helen 22 Jahre alt.

Für kleine Matheasse kann das Binärsystem auch sehr spannend sein. Paul konnte zum Beispiel als Vorschulkind mit 6 Jahren nur mit den Fingern einer Hand bis 31 zählen. Finger ausgestreckt bedeutete 1 und Finger eingeknickt bedeutete 0. Also symbolisierten alle ausgestreckten Finger seiner Hand die Binärzahl 11111 und dies sind 31 (16+8+4+2+1). Faszinierend oder? (Besonders reizvoll für Kinder ist die Bedeutung des „Stinkefinkers“, also die Binärzahl 00100. Na weißt du welche Zahl es im Dezimalsystem ist?)

Zwei hoch vier

Zwei hoch drei

Zwei hoch zwei

Zwei hoch eins

Zwei hoch Null

Binärzahl

Dezimalzahl

11111

00100

???

Nach diesem System kann man also die Jahreszahl 2017 folgendermaßen in das System der Dualzahlen (Binärzahlen) übertragen:

1024	512	256	128	64	32	16	8	4	2	1
1	1	1	1	1	1	0	0	0	0	1

Binärzahl: 11111100001

Dezimalzahl: 1024+512+256+128+64+32+1 = 2017

Als einen letzten Tipp habe ich noch die klassischen Hölzchenknobeleien. Lege doch mal die Zahl 2017 mit Zahnstochern, Streichhölzchen oder ganz ungefährlich mit Wattestäbchen. Und nun könnt ihr euch selbst kreativ Knobelaufgaben dazu ausdenken, wie z.B. Wie viele Wattestäbchen musst du wie umlegen, um die größtmögliche oder die kleinstmögliche Zahl zu erhalten?

Na habt ihr Lust bekommen auf Zahlenforscherreise mit euren kleinen Matheforschern zu gehen? Dann probiert es aus und lasst euch überraschen, welche tollen Ideen sie entwickeln werden. Gern könnt ihr mir wieder schreiben, was es spannendes zu entdecken gab. Ich freue mich und wünsche euch allen viel Gesundheit und Glück in eurem wundervollen Jahr 2017!

Eure Mandy Fuchs

Alltagsmathematik, Eltern, Grundschule, Kinder unter 3 Jahren

Weihnachtszeit – Zeit zum Spielen

2016-12-11 mandyfuchs Hinterlasse einen Kommentar

Gerade jetzt wo die Tage eigentlich viel zu kurz erscheinen und wo es schon am Nachmittag draußen so dunkel ist, wie sonst spät am Abend, haben wir viele Möglichkeiten, es uns im Haus gemütlich zu machen. Wie wäre es, gemeinsam mit den Kindern Bücher anzuschauen, zu lesen, zu puzzeln oder zu spielen? Kinder lernen viele Dinge im Spiel und das gemeinsame Spielen von Eltern mit ihren Kindern und der Kinder untereinander ist so bedeutungsvoll, nicht nur für das Lernen von Mathematik. Durch das Spiel setzen sich Kinder auf ihre ganz eigene Weise mit der realen Welt, mit Fragen, Gedanken und Gefühlen auseinander. Das Spiel sensibilisiert ihre Wahrnehmungsfähigkeit, ihre Selbstständigkeit und ihre Selbstwirksamkeit. Und dafür gibt es so viele verschiedene Spiele: Fingerspiele, Kniereiterspiele, Bauspiele, Entdeckungs- und Wahrnehmungsspiele, Konstruktionsspiele, Spiele zum Gestalten, Bewegungsspiele, Musikspiele, Handpuppen- und Marionettenspiele, Schattenspiele, Gesellschaftsspiele, Austobespiele, Rollenspiele, Theaterspiele, Märchenspiele, Magnetspiele und auch Logik- und Denkspiele.

Was macht das Spiel so bedeutsam für die kindliche Entwicklung? Ich kann es dir sagen: Es sind die wertvollen Merkmalen des Spiels, wie z.B.:

die intrinsische Motivation (das Spielbedürfnis kommt vom Spielenden selbst) und der Selbstzweck des Spiels,
die Loslösung vom Alltag (Kinder dürfen selbst in andere Rollen schlüpfen) und das Ausleben der Fantasie,
die Selbstbestimmung und Selbstkontrolle der Spielenden,
die Beteiligung der Emotionalität (Spielen macht Spaß), je offener die Bewältigung der Spielaufgabe ist, desto größer ist der Reiz beim Spielen und somit auch die lustvolle Spannung,
der vorher nicht immer bekannte bzw. bestimmte Ausgang beim Spielen,
die Notwendigkeit von Ordnung und Sicherheit gebenden (Spiel)Regeln,
die Wiederholung und das Ritual im Spiel sowie
das Erleben von Gemeinsamkeit zwischen den Spielenden.

Und da ich ja in einem vorherigen Beitrag geschrieben habe, sich mit Mathematik zu beschäftigen kann wie ein Spiel sein (vgl. hierzu auch den Numeracy-Ansatz), möchte ich dir heute ein paar ausgewählte mathematische Spiele nicht nur für die Weihnachtszeit vorstellen, denn eins ist für mich ganz klar: Kinder dürfen mit Mathematik jederzeit spielen und sie sollen sogar die Möglichkeit erhalten, nicht nur in der Kita sondern auch in der Grundschule und zu Hause, mathematische Phänomene spielerisch zu entdecken und zu erforschen. Ich stelle euch aus allen drei Altersbereichen (Krippe, Kindergarten, Grundschule) jeweils meine drei Favoriten vor (was gar nicht so leicht war auszuwählen). Viele weitere Tipps für Spiele findest du hier.

Spiele für Matheforscher im Krippenalter

Dieses Motorikspielzeug (Manhattan Toy 200970 – Skwish Motorikschleife) gehört für mich mit zu den Highlights im Babyspielzeugbereich. Das Spielzeug aus nachwachsendem Gummibaumholz (mit wasserbasierten, ungiftigen Farben hergestellt) fasziniert schon die kleinsten Matheforscher mit seinem beweglichen Netz aus Stangen, Schnüren und Kugeln. Babys können es drücken und dehnen und begeistert zusehen, wie es langsam wieder in seine ursprüngliche Form zurückkehrt. Das klassische Holzspielzeug stimuliert den Sehsinn, hilft kleinen Matheforschern bei der Entwicklung motorischer Fähigkeiten und fördert das Wahrnehmen mit allen Sinnen.

Mein eigentliches Highlight für Kinder im Krippenbereich (und darüber hinaus) ist der große Regenbogen von Grimm`s Spiel und Holz Design. Ein Kreativitätsspielzeug aus Holz, was durch seine scheinbare Einfachheit erst im und durch das Spiel kleiner Matheforscher sein ungemeines Potenzial entfaltet. Das Spiel mit dem Regenbogen fördert neben der Kreativität der Kinder auch ihre Problemlösefähigkeit, ihre Fein- und Grobmotorik, ihr räumliches Denken, Mengen- und Größenvorstellungen und vieles andere mehr.

Und meine Nummer drei sind Magnetspielzeuge, wie zum Beispiel das magnetische Konstruktionsspielzeug (z.B. von Magformers oder Supremery). Dieses moderne Bauspielzeug, bestehend aus ineinander greifenden magnetischen Kunststoff-Formen eröffnet Matheforschern ab dem Krippenalter eine Welt der Möglichkeiten für ein fantasievolles und kreatives Spielen. Es können geometrische Körpermodelle, Gebäude, Fahrzeuge oder sonstige Fantasieobjekte gebaut werden. Wenn Kinder die magnetischen Bausteine verwenden, spielen sie nicht nur, sondern entwickeln ihre eigenen Fähigkeiten und Kompetenzen weiter, wie
–        kreatives Denken,
–        Mustererkennung,
–        Feinmotorik,
–        Augen-Hand-Koordination,
–        Problemlösekompetenz,
–        Entscheidungen treffen,
–        soziale Fähigkeiten,
–        erforschen von Konzepten und Größen,
–        erfahren von Ursache und Wirkung und ihr
–        räumliches Denkvermögen.

Spiele für Matheforscher im Kindergartenalter

Mein erster Tipp sind die vielfältigen Nikitin-Materialien, z.B. die Musterwürfel. Hier werden nicht nur Wahrnehmung, Sinneserfahrung und räumliches Vorstellungsvermögen gefördert, sondern auch feinmotorische Fähigkeiten und kreatives Gestalten. Mit nur 16 Musterwürfeln haben kleine Matheforscher die Möglichkeiten, Muster zu legen, nach Vorlagen zu bauen und zu konstruieren. Jedes Kind kann seinem Lernniveau entsprechend gefördert werden und immer wieder eigene Spielideen entwickeln.

Mein zweiter Tipp sind zwei Klassiker: nämlich die Spiele „Vier gewinnt“ und „Tic-Tac-Toe“, allerdings in ihren jeweiligen 3-D (dreidimensionalen) Ausführungen in ansprechender Holzgestaltung. Gefordert sind bei beiden Spielen Strategie und Taktik. Gefördert werden u.a. die genaue Beobachtungsgabe, Konzentration, das logische Denken sowie das räumliche Vorstellungsvermögen. Zwei Spiele für kleine Matheforscher und interessierte Matheasse.

Auch im Kindergartenbereich habe ich einen Tipp für ein magnetisches Spielzeug: den Magnetwürfel. Wie von Geisterhand bleiben die 24 Teile „kleben“ oder eben nicht… wie geht das? Die Kinder sind immer wieder fasziniert und probieren aus. Die magnetischen Wedges führen unweigerlich zur Beschäftigung mit ihnen und zum kreativen Konstruieren. Durch die Abstraktion und Einfachheit der Bauteile sind eine Fülle von Formen und Figuren umsetzbar: Kronen, Diamanten, Fahrzeuge, Tiere, Häuser und vieles mehr. Kleine Matheforscher können frei oder nach Anleitungen bauen, was beides sehr reizvoll sein kann. Und am Ende entwickeln sie ihre eigenen Strategien, den Würfel wieder in seine ursprüngliche Gestalt zusammen zu setzen.

Spiele für Matheforscher im Grundschulalter

Mein persönliches Lieblingsspiel ist Qwirkle, Spiel des Jahres 2011! Ich liebe es und spiele es selbst sehr gern in meiner Familie. Dieses fesselnde und bereits mehrfach ausgezeichnete Kombinationsspiel setzt auf denkbar einfache Regeln und schon in wenigen Minuten hat man das Spielprinzip verstanden. Jeweils dreimal 36 haptisch sehr ansprechenden Spielsteinen aus Holz, die sich durch sechs verschiedene Symbole und Farben unterscheiden sind im Spiel. Damit bilden und erweitern die Spieler Reihen gleicher Farben oder gleicher Symbolform. Dafür gibt’s Punkte. Mal drei, mal 12, mal gar keine… Mit den Erweiterungen ergeben sich vielfältige Variationsmöglichkeiten, da die Erweiterungen untereinander kombinierbar sind. So lässt sich Qwirkle auf viele verschiedene Arten spielen.

Mein Tipp Nummer zwei in dieser Kategorie ist eigentlich auch bereits ein Klassiker: Ubongo. Jeder Spieler hat eine Legetafel und 12 Legeteile (dies sind Teile, die aus zwei, drei oder mehr Einheitsquadraten bestehen) vor sich liegen. Es wird gewürfelt und die Sanduhr umgedreht. Alle versuchen, ihre Tafel so schnell wie möglich mit den angegebenen Teilen lückenlos zu belegen. Wer dies schafft, ruft „Ubongo“ und wird mit Edelsteinen belohnt. Kleine und große Matheforscher fördern mit diesem Spiel ihr räumliches Vorstellungsvermögen ungemein.

Und mein Tipp Nr.3 ist ein Spiel für einen kleinen Matheforscher allein: Rush Hour. Zu Beginn des Knobelspiels steht der Spieler mit seinem kleinen roten Auto im Stau. Ziel ist, sich einen Weg zur Ausfahrt zu bahnen. Auf 40 verschiedene Arten ist der Wagen zu Beginn verkeilt, jede Aufgabe ist eine neue Herausforderung. Spannend wird es, weil die Ausgangssituation langsam immer kniffliger wird. Der Ehrgeiz treibt den Spieler, jeweils die nächste, etwas schwierigere Aufgabe zu knacken. Dabei legt das Gehirn den Turbogang ein und der Spieler trainiert sein strategisches Denken, sein räumliches Vorstellungsvermögen sowie das vorausschauende Sehen und Kombinieren.

Abschließend möchte ich für dich noch folgende Frage beantworten.

Nach welchen Kriterien sollte ich Spielmaterialien und Spiele auswählen?

Um die enorme Kraft des Spiels zu unterstützen, kommt der Auswahl geeigneter Spielmaterialien eine immer stärkere Bedeutung zu. Hinzu kommt, dass die Spielzeugindustrie und zahlreiche Spielsachenhersteller den Markt scheinbar „überschütten“ und mit geschickten Marketingstrategien zu manchmal unbedachten Käufen anregen. Wichtige Aspekte zur Auswahl geeigneter Dinge zum Spielen für die Kinder kann ich für dich so zusammenfassen:

Interesse des Kindes: Durch Beobachten erfahren erwachsene Lernbegleiter die Themen und Interessen der Kinder, nach denen sie sich bei der Anschaffung orientieren können. Diese sind immer wieder verschieden, so dass bestimmte Spielmaterialien auch innerhalb der Kita nur einmal angeschafft werden müssen und dann je nach den Bedürfnissen der Kinder „wandern“ können.
Alter und Fähigkeiten, Anknüpfen an Lebenserfahrungen, Alltagsbezug der Kinder: Die ausgewählten Spiele sollten sich zwar grob am jeweiligen Alter der Kinder orientieren aber vor allem auch die individuelle Kompetenzentwicklung des Kindes berücksichtigen. Es kann durchaus sein, dass ein fünfjähriges Kind bereits Schach spielen kann und deshalb ein Schachspiel und einen geeigneten Spielpartner benötigt. Viele kleine Matheforscher sind z.B. auch schon bereits im Kindergarten von Zahlen und vom Zählen begeistert, so dass sie z.B. mit vielen Ziffern aus Holz ihre Lieblingszahlen oder ihre Hausnummer oder andere für sie bedeutsame Zahlenmuster legen und es lieben viele gleiche Dinge abzuzählen.
Kreative, vielseitige, fortwährende Spielmöglichkeiten, Förderung von Vorstellungsvermögen: Spielzeug ist dann besonders geeignet, wenn es zu vielfältigen fantasievollen Spielideen anregt und nicht nur eingeschränkt auf eine Art oder Funktion des Spielens reduziert wird. Kinder werden schnell die Freude am Spiel verlieren, wenn das Spielzeug z.B. auf Knopfdruck nur ein Geräusch von sich gibt. Hingegen erzeugen z.B. magnetische Baumaterialien oder Baukastensysteme immer wieder neue Spielreize und fördern zudem ganz nebenbei das räumliche Vorstellungsvermögen kleiner Matheforscher.
Gestaltung, Farbe, Form: Kinder lieben Farben, dennoch sind diese sparsam und mit Bedacht einzusetzen. Der heutzutage sowieso reizüberfluteten Umwelt der Kinder entgegen wirkt das Kriterium „weniger ist mehr“. Das heißt Spielsachen, die weniger bunt sind, die weniger sinnlose Verzierungen oder weniger unnötige Formen aufweisen sind für Kinderhände und Kinderaugen geeigneter. Gerade z.B. schlichte Holzspielsachen bieten den Kindern vielfältige Auseinandersetzungs- und Gestaltungsmöglichkeiten.
Haltbarkeit, Lebensdauer, Sicherheit und Umweltverträglichkeit: Dies sind Kriterien, die innerhalb unserer Wegwerf- und Konsumgesellschaft nicht häufig genug betont werden können. Spielmaterialien für Kinder sollten deshalb stets für Kinderhände und Kindermünder sicher sein (frei von Schadstoffen sein, keine Verletzungsgefahr auslösen), die Umwelt nicht zusätzlich belasten (mehr aus wenig oder unbehandelten natürlichen Materialien als aus Kunststoff bestehen) und langlebig sein.

Na, konnte ich deine eigene Spiellust wieder ein wenig heraus kitzeln? Dann schau doch, ob du vielleicht das ein oder andere Spiel noch auf deinen Weihnachtswunschzettel (oder den deiner Kinder) setzen möchtest. Auf alle Fälle wünsche ich dir eine besinnliche (Vor)Weihnachtszeit, viel gemeinsame Spielzeit mit deinen Kindern und immer kreative Spielideen. Lass von dir hören!

Mandy Fuchs

Alltagsmathematik, Kinder unter 3 Jahren

Kleine Matheforscher in Windeln?

2016-12-03 mandyfuchs Hinterlasse einen Kommentar

Ich werde immer wieder gefragt, wie Mathematik im Krippenalter (also im Alter von 0 bis 3 Jahren) umgesetzt werden kann. Um es gleich vorweg zu nehmen: Die Förderung mathematischer Kompetenzen von Kindern im Krippenalter ist nicht an bestimmte Programme oder Materialien gebunden. Vielmehr gilt es genau zu schauen, was Säuglinge, Babys und Kleinkinder eigentlich von Geburt an bereits mitbringen und herauszufinden, was sie von uns erwachsenen Lernbegleitern demzufolge brauchen.

Zunächst stelle ich dir hier kurz einige Studienergebnisse aus der Säuglingsforschung vor. Keine Angst, du wirst sie verstehen und sie werden dich beeindrucken. (Nachzulesen bei Fthenakis u.a. 2009. Natur-Wissen schaffen. Band 2: Frühe mathematische Bildung. Troisdorf: Bildungsverlag EINS. S. 84f.)

Kinder bringen von Geburt an die Voraussetzungen und die Bereitschaft sowohl für das Erlernen der Sprache als auch für die Erschließung der Welt der Zahlen mit. Man weiß durch Studien, dass sich Babys zum Beispiel schon mit etwa vier Monaten für die Anzahlen von Dingen interessieren und sogar drei bis vier Gegenstände voneinander unterscheiden können. Du fragst dich vielleicht, wie Forscher dies herausfinden können. Durch die Habituationsmethode. In Experimenten nach dieser Methode wird den Kindern ein „visueller Reiz“, z.B. Bilder mit immer zwei Dingen, mehrere Male nacheinander gezeigt. In der Regel ist das Interesse des Kindes an den Bildern anfänglich hoch und nimmt dann allmählich ab. Dies zeigt sich darin, dass die Bilder nach und nach immer kürzer angeblickt werden (Habituation bzw. Gewöhnung). Werden dann jedoch Bilder mit immer drei Dingen gezeigt, steigt die Blickzuwendung des Kindes in der Regel wieder an (Dishabituation bzw. Neuheitsreaktion). Dies geschieht natürlich nur dann, wenn das Kind einen Unterschied zwischen den Bildern erkannt hat. Ein solches intuitives Zählen basiert auf der automatisierten Fähigkeit, kleine Mengen „auf einen Blick“ erfassen zu können. Man nennt dies auch die Fähigkeit Mengen simultan erfassen zu können. Im Englischen verwendet man hierfür den Begriff subitizing. Auch durch das differenzierte Wahrnehmen von Bewegungen unterscheiden Babys kleine Anzahlen. In einem Experiment zeigte man ihnen einen Stoffhasen, der immer wieder zweimal hüpft. Schnell verloren sie das Interesse. Als der Hase jedoch dreimal hüpfte, waren sie sofort wieder aufmerksam. In einem anderen Experiment zeigte man fünf Monate alten Kindern folgendes: Sie sahen zunächst auf der linken Hälfte eines Computerbildschirms ein Bild zweimal und dann auf der rechten Seite des Bildschirms dreimal ein Bild. Was geschah? Nach mehreren Durchläufen zählten die Babys mit. Nachdem das Bild zweimal links zu sehen war, schauten sie sofort nach rechts und als es dort dreimal erschienen war, ging ihr Blick sofort wieder nach links. Genial oder?

Es wird noch erstaunlicher! Pass auf! Fünf Monate alte Kinder zeigen sogar schon ein Gespür fürs intuitive Rechnen, also ein grundlegendes Verständnis für wesentliche Prinzipien der Addition und Subtraktion im Bereich von drei Gegenständen. Wie das? Babys erwarten, dass eine Anzahl größer wird, wenn man etwas hinzufügt und auch, dass eine Anzahl kleiner wird, wenn man etwas wegnimmt. Dies hat man ebenfalls mit einem Habituations-Experiment herausgefunden: Eine Figur wird vor den Augen des Kindes in einen nach vorne hin offenen Kasten gestellt. Nun kommt genau vor die Figur eine Abdeckung, so dass sie nicht mehr zu sehen ist. Eine zweite Figur wird für die Kinder deutlich sichtbar hinter die Abdeckung geschoben, also hinzugefügt. Die Hand verschwindet leer aus dem Sichtfeld des Kindes. In der Versuchsanordnung konnte man nun für das Kind unsichtbar diese zweite Figur entfernen oder eben auch nicht. Wurde die Abdeckung nun entfernt, sah das Kind entweder eine oder zwei Figuren. Was passierte? Die Kinder fanden es völlig „normal“ und eher uninteressant, wenn sie genau das sahen, was sie erwartet haben. Aber sie reagierten immer dann überraschter und interessierter, wenn die Anzahl der Figuren nicht mit der Handlung übereinstimmte. Sie „wunderten“ sich also, wenn nur eine Figur zu sehen war, obwohl doch offensichtlich jemand eine weitere hinzugefügt hatte. Wenn man eine Figur von zweien wegnahm und danach trotzdem noch zwei Figuren zu sehen waren, entstand der gleiche „Überraschungseffekt“. Na was sagst du zu unseren kleinsten Matheforschern?

Die umfangreichen entwicklungspsychologischen Forschungen der letzten Jahrzehnte belegen viele solcher erstaunlichen und differenzierten Kompetenzen von Kindern im Alter von 0 bis 3 Jahren. Das Bild des Säuglings hat sich dadurch radikal verändert. Kinder sind von Geburt an mit Neugier und Kompetenzen ausgestattet, die Welt um sich herum zu erkunden und sie sich spielend anzueignen. Ja genau: durch SPIELEN! (Tipps zu Spielen für kleine und große Matheforscher findest du hier.) Aber da gehen wir später in den Praxisbeispielen nochmal drauf ein.

Du merkst also ganz deutlich: Heute wird stärker denn je auf das kompetente Kind verwiesen, welches bereits etwas kann und seine Entwicklung intensiv mitbestimmt (vgl. auch meine Ausführungen zum Kindbild). Dass die Entwicklungsprozesse in soziale Prozesse sowie in einen kulturellen Kontext eingebunden sind, ist in dieser Diskussion unstrittig. Im Gegenteil: Die soziale Dimension des Aufwachsens von Kindern wird ganz besonders betont: Niemand kann in Isolation leben und heranwachsen, Kinder brauchen Bindungspersonen und Gemeinschaften, in denen sie sich wohl und aufgehoben fühlen, denn ohne Bindung kann keine Bildung stattfinden. Säuglinge, Babys und Kleinkinder sind von Geburt an also nicht so hilflos wie du vielleicht angenommen hast, sondern so ausgestattet, dass sie sich durch sinnliche Erfahrungen ein eigenes Bild von der Welt machen können. Auch von der mathematischen Welt! Ausgangspunkt ihrer kindlichen Welterforschung sind deshalb in aller erster Linie Körpererfahrungen: Kinder wollen mit allen Sinnen lernen, die (mathematische) Welt „begreifen“ und ihren Bewegungsdrang ausleben.

Was heißt dies nun bezogen auf das mathematische Lernen von Krippenkindern?

Als Brückenpfeiler einer mathematischen Früherziehung innerhalb des Krippenalltags gelten das Sortieren und Ordnen; Formen, Farben und Muster; Raum- und Körpererfahrungen sowie Erfahrungen mit Zahlen, im Zählen und im Messen. Hierbei kommt dem Wahrnehmen über alle Sinnesbereiche (Tast- und Spürsinn; Bewegungs-, Kraft- und Stellungssinn; Gleichgewichtssinn; Geschmackssinn; Geruchssinn; Hörsinn und Sehsinn) eine große Bedeutung zu. Darauf würde ich in einem späteren Blogbeitrag noch einmal ausführlicher eingehen wollen.

Eine Möglichkeit für den Einstieg ins Klassifizieren, Sortieren und Zuordnen sind die täglichen Aufräumrituale. Daraus kann z.B. ein Kategorisierungsspiel gemacht werden, indem die Kinder herausfinden, was wohin gehört. Mit den Kindern können auch Dinge des Alltags gesammelt und nach ihren verschiedenen Eigenschaften sortiert und verglichen werden. So differenzieren sie Steine, Muscheln oder Blätter, aber auch Alltagsgegenstände wie Plastikbecher, Kisten, Kartons und Papiertüten laden zum Abstrahieren und Gruppieren ein. Jedes Kind verfolgt sein eigenes Ordnungssystem, das sich an sehr unterschiedlichen Kriterien orientieren kann: Verwendungszweck (Kochen, Essen, Putzen), Formen (rund, eckig, gerade), Farben (von bunt nach grau) oder auch Gefühlen (von lustig nach langweilig). Mathematische Bildung geschieht, wenn wir zusammen mit den Kindern immer wieder neue Muster, Formen und Mengen im Alltagshandeln entdecken und benennen.

Einen großen Raum nimmt jedoch das Spiel der Kinder ein. Im Folgenden sollen hierfür einige Beispiele aus der Praxis vorgestellt werden:

Alltagmaterialien, wie hier die Korken, Nudeln, Kastanien und Walnüsse sowie die Vorhangringe, werden zu äußerst anregenden Lern- und Spielumgebungen für kleine Matheforscher, wenn sie mit ausgewählten Schüsseln, Bechern, Löffeln, Flaschen, Dosen usw., kombiniert werden. Sie regen die Kinder an, im Spiel ein- und umzufüllen, auszuschütten, reinzustecken und dabei mit allen Sinnen Erfahrungen mit Mengen zu machen. Die Kinder beschäftigen sich so mit ihren eigenen Forscherfragen, z.B. Wie viele Nudeln passen in den Becher? Wie hört es sich an, wenn viele oder nur wenige Nüsse in der Flasche sind? Ist ein Becher mit Korken genauso schwer wie ein Becher mit Kastanien? Wie muss ich den Ring drehen, damit er in die Dose passt? …

Die Auseinandersetzung mit diesen Themen bietet den kleinsten Matheforschern also bereits die Möglichkeit, vielfältige Erfahrungen zu bedeutsamen mathematischen Basiskompetenzen zu sammeln, wie z.B. das Erkennen der Mengeninvarianz (dies meint die Unveränderbarkeit von Mengen), die räumliche Orientierung (oben, unten, rechts, links, …), die Figur-Grund-Diskriminierung (dies meint einzelne Dinge aus einer Menge von unterschiedlichen Gegenständen herauszufinden), die Auge-Hand-Koordination, das Erfassen und Wahrnehmen von Größen (Länge, Gewicht, Zeit, Volumen, Geld) oder das Erkennen von Teil-Ganzes-Beziehungen.

Sandwannen bzw. –tische tragen ebenfalls dazu bei, sinnliche Erfahrungen im Spiel zu machen und als kleine Forscher Spuren zu hinterlassen.

Auf diesen Fotos werden weitere Möglichkeiten für das Sammeln mathematischer Basiskompetenzen von Matheforschern unter drei Jahren sichtbar. Wenn die Kinder die Hocker der Größe nach ordnen, um darauf zu klettern und runter zu springen, bilden sie Reihenfolgen. Die Stifte werden nach dem Malen nach Farben sortiert. Alle Bälle kommen nach dem Spielen (rollen, prellen, schießen, werfen, …) in die Ballkiste (nicht zu den Bausteinen). Und warum passt ein Ball nicht in die Kiste?

Zahlreiche Spielmaterialien sind sehr gut geeignet, dass kleine Matheforscher Muster entdecken und selbst herstellen (stecken, bauen, legen, auffädeln, …) und hierbei differenzierte visuelle Erfahrungen mit Raum, Form und Farbe machen. Wenn Materialien zudem noch magnetisch sind, üben sie eine besondere Faszination auf die Kinder aus und fördern ganz nebenbei ihre Konzentration und Ausdauer.

Zahlreiche Bilderbücher regen schon die kleinsten Matheforscher an, die Welt der Zahlen, Formen, Größen, Muster und Figuren zu entdecken. Neben vielen mathematischen Kompetenzen werden beim dialogischen Bilderbuchbetrachten ebenso ihre Sprachkompetenzen gefördert. Hierbei sind Bilderbuchklassiker wie z.B. Die kleine Raupe Nimmersatt, Elmar und Morgens früh um 6 aber auch Wimmelbücher und Quietbooks wunderbar geeignet. Als Fachbuch kann ich euch Formen, Muster, Mengen – Mathe in der Krippe (Jeanette Boetius) empfehlen.

Mein Fazit: Kleine Matheforscher kommen neugierig und wissenshungrig auf die Welt, setzen all ihre Energie ein, um ihren Hunger auf Entdeckungen und neue Erfahrungen zu stillen. Sie erwerben in ihren ersten Lebensjahren die wichtigsten Denkstrukturen, die sie für ihr gesamtes späteres Leben brauchen, nicht nur für das Lernen von Mathematik. Kleine Matheforscher lernen vor allem durch das Spiel und durch das eigene selbständige Tun und Handeln in einem anregenden Umfeld. Sie lernen in ko-konstruktiven Prozessen, das heißt sie brauchen Erwachsene (dich) und andere Kinder zum gemeinsamen Spielen und Forschen.